题目内容
11．已知一组数据x1，x2，x3，x4的平均数是5，则数据x1+3，x2+3，x3+3，x4+3的平均数是8．分析 根据平均数的性质知，要求x1+3，x2+3，x3+3，x4+3的平均数，只要把数x1，x2，x3，x4的和表示出即可．
解答 解：∵x1，x2，x3，x4的平均数为5
∴x1+x2+x3+x4=4×5=20，
∴x1+3，x2+3，x3+3，x4+3的平均数为：
=（x1+3+x2+3+x3+3+x4+3）÷4
=（20+12）÷4
=8，
故答案为：8．
点评 本题考查的是算术平均数的求法．解决本题的关键是用一组数据的平均数表示另一组数据的平均数．
练习册系列答案
相关题目
证明命题“角的平分线上的点到角的两边的距离相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．
19．
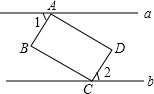如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（ ）
如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
6．下列图形中，是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
16．2的绝对值是（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
两个全等的三角尺重叠放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F．已知∠ACB=∠DCE=90°，∠B=30°，AB=8cm，则CF=2$\sqrt{3}$cm．
1．
如图，所示是二次函数y=ax2+bx+c图象的一部分，图象过点A（5，0），对称轴为直线x=1，下列结论中错误的是（ ）
如图，所示是二次函数y=ax2+bx+c图象的一部分，图象过点A（5，0），对称轴为直线x=1，下列结论中错误的是（ ）| A． | abc＞0 | B． | 当x＜1时，y随x的增大而增大 | ||
| C． | a+b+c＞0 | D． | 方程ax2+bx+c=0的根为x1=-3，x2=5 |