题目内容
8.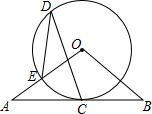 如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F.
如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F.(1)求证:AE=BF;
(2)若D是优弧EF上一点,连接DE,DC,$\frac{OB}{AB}$=$\frac{5}{8}$,求tan∠CDE的值.
分析 (1)利用等腰三角形的判定得到OA=OB,然后两边都减去半径即可得到结论;
(2)作直径CG,连接EG,连接EF交CG于H,如图,先证明∠CEH=∠CDE,设OB=5x,AB=8x,则AC=BC=4x,再利用勾股定理计算出OC,接着利用相似比计算出EH、OH,从而得到CH的长,然后利用正切的定义求解.
解答 (1)证明:∵∠A=∠B,
∴OA=OB,
∴OA-OE=OB-OF,
即AE=CF;
(2)解:作直径CG,连接EG,连接EF交CG于H,如图,
∵CG为直径,
∴∠CEG=90°,
∵AB与⊙O相切于点C,
∴OC⊥AB,
∴∠ECG=90°,
∴∠ACE=∠G,
而∠G=∠CDE,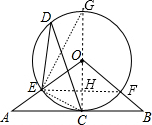
∴∠ACE=∠CDE,
∵OE:AE=OF:BF,
∴EF∥AB,
∴∠ACE=∠CEH,EF⊥OC,
∴∠CEH=∠CDE,
由$\frac{OB}{AB}$=$\frac{5}{8}$,设OB=5x,AB=8x,则AC=BC=4x,
在Rt△AOC中,OC=$\sqrt{(5x)^{2}-(4x)^{2}}$=3x,
∵EH∥AC,
∴$\frac{EH}{AC}$=$\frac{OH}{OC}$=$\frac{OE}{OA}$,即$\frac{EH}{4x}$=$\frac{OH}{3x}$=$\frac{3x}{5x}$,解EH=$\frac{12}{5}$x,OH=$\frac{9}{5}$x,
∴CH=OC-OH=3x-$\frac{9}{5}$x=$\frac{6}{5}$x,
在Rt△CEH中,tan∠CEH=$\frac{CH}{EH}$=$\frac{\frac{6}{5}x}{\frac{12}{5}x}$=$\frac{1}{2}$,
∴tan∠CDE的值为$\frac{1}{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决(2)小题的关键是证明∠CEH=∠CDE.

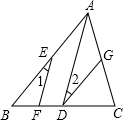 已知:如图,AD∥EF,∠1=∠2,判断AB与DG的位置关系,并说明理由.
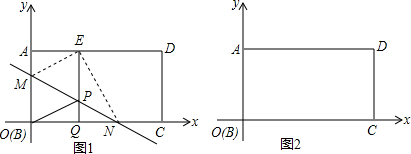
已知:如图,AD∥EF,∠1=∠2,判断AB与DG的位置关系,并说明理由.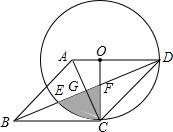 如图,已知菱形ABCD中,AD∥BC,AD=$\sqrt{2}$,点O是AD上一点,以O为圆心,OD长为半径的⊙O与BC相切于点C,与BD相交于点E,连接OC,AC,分别与BD相交于点F,G.
如图,已知菱形ABCD中,AD∥BC,AD=$\sqrt{2}$,点O是AD上一点,以O为圆心,OD长为半径的⊙O与BC相切于点C,与BD相交于点E,连接OC,AC,分别与BD相交于点F,G.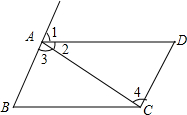 如图,由下列条件可以判定图中哪两条直线平行,说明理由
如图,由下列条件可以判定图中哪两条直线平行,说明理由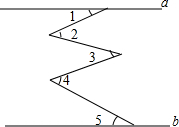 如图,a∥b,试探究∠1,∠2,∠3,∠4,∠5的数量关系.
如图,a∥b,试探究∠1,∠2,∠3,∠4,∠5的数量关系. 如图,l1∥l2,∠ABC=120°,l1⊥AB.
如图,l1∥l2,∠ABC=120°,l1⊥AB.