题目内容
14.把下列各式化为不含负指数幂的形式(1)$\frac{1}{2}$a3b-2c-3=$\frac{{a}^{3}}{2{b}^{2}{c}^{3}}$
( 2 )(x-1+y-1)-1$\frac{xy}{x+y}$.
分析 根据负整数指数幂与正整数指数幂互为倒数,可得答案.
解答 解:(1)$\frac{1}{2}$a3b-2c-3=$\frac{{a}^{3}}{2{b}^{2}{c}^{3}}$
( 2 )(x-1+y-1)-1 $\frac{xy}{x+y}$,
故答案为:$\frac{{a}^{3}}{2{b}^{2}{c}^{3}}$,$\frac{xy}{x+y}$.
点评 本题考查了负整数指数幂,利用负整数指数幂与正整数指数幂互为倒数是解题关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
5.△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②a2=(b+c)(b-c);③a:b:c=5:12:13.其中能判断△ABC是直角三角形的个数有( )
| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
4.对于非零的实数a,b,规定a?b=$\frac{1}{b}$$-\frac{1}{a}$,若2?(2x-1)=1,则x=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{6}$ | D. | $-\frac{1}{6}$ |
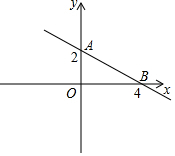 如图,直线AB与x轴,y轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.问题:
如图,直线AB与x轴,y轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.问题: 如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.
如图,在△ABC中,∠C=90°,AE平分∠A交BC于E,CD⊥AB于D,交AE于F,FM∥AB交BC于M,求证(1)$\frac{AE}{AF}=\frac{AB}{AC}$;(2)$\frac{EB}{MB}=\frac{AE}{AF}$;(3)CE=BM.