题目内容
19.关于x的方程x2+ax+a=0的根都是整数,求符合条件的a的整数值.分析 由△=a2-4a≥0,得到a≥4或a≤0,根据根与系数的关系得到x1+x2=-a.x1•x2=a,∴x1+x2+x1•x2=0,于是得到x1+x2+x1•x2+1=1,即可得到结论.
解答 解:∵x的方程x2+ax+a=0的根都是整数,
∴△=a2-4a≥0,
∴a≥4或a≤0,
∵x1+x2=-a.x1•x2=a,
∴x1+x2+x1•x2=0,
∴x1+x2+x1•x2+1=1,
∴(x1+1+)(x2+1)=1,
∵x1,x2为整数,
∴$\left\{\begin{array}{l}{{x}_{1}+1=1}\\{{x}_{2}+1=1}\end{array}\right.$,或$\left\{\begin{array}{l}{{x}_{1}+1=-1}\\{{x}_{2}+1=-1}\end{array}\right.$,
∴x1=x2=0,或x1=x2=-2.
∴a=0或a=4.
点评 本题考查了一元二次方程根的判别式,根与系数的关系,正确的理解题意是解题的关键.

练习册系列答案
相关题目
8.如果关于x的分式方程$\frac{ax}{x-1}$+$\frac{1}{x+2}$=0有增根,那么增根可能是( )
| A. | x=1 | B. | x=-2 | C. | x=1或x=-2 | D. | 无法确定 |
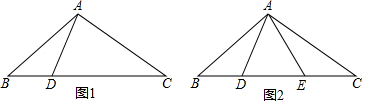
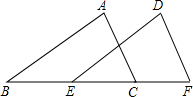 如图,已知△ABC≌△DEF,AB与DE是对应边,∠ACB与∠F是对应角.
如图,已知△ABC≌△DEF,AB与DE是对应边,∠ACB与∠F是对应角.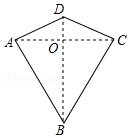 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角.
我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角.