题目内容
3.先化简,再求值:($\frac{1}{x-2}$+$\frac{1}{x+2}$)÷$\frac{{x}^{2}}{{x}^{2}-4}$,其中x=$\sqrt{2}$.分析 根据分式的混合运算法则把原式化简,根据二次根式的除法法则计算即可.
解答 解:($\frac{1}{x-2}$+$\frac{1}{x+2}$)÷$\frac{{x}^{2}}{{x}^{2}-4}$
=$\frac{x+2+x-2}{{{x^2}-4}}•\frac{{{x^2}-4}}{x^2}$
=$\frac{2}{x}$,
当$x=\sqrt{2}$时,原式=$\frac{2}{{\sqrt{2}}}$,
=$\sqrt{2}$.
点评 本题考查的是分式的化简求值,掌握分式的混合运算法则是解题的关键.

练习册系列答案
相关题目
8.如果关于x的分式方程$\frac{ax}{x-1}$+$\frac{1}{x+2}$=0有增根,那么增根可能是( )
| A. | x=1 | B. | x=-2 | C. | x=1或x=-2 | D. | 无法确定 |
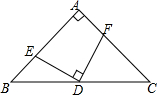 如图,在△ABC中,AB=AC,∠BAC=90°,D是BC中点,ED⊥FD,ED与AB交于E,FD与AC交于F.若BE=4cm,CF=6cm,则S△ABC=50cm2.
如图,在△ABC中,AB=AC,∠BAC=90°,D是BC中点,ED⊥FD,ED与AB交于E,FD与AC交于F.若BE=4cm,CF=6cm,则S△ABC=50cm2.


