题目内容
10.在?ABCD中,对角线AC、BD交于O点,AC=6,BD=2,设AB的长为x,将x的取值范围在数轴上表示正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 首先由在?ABCD中,对角线AC、BD交于O点,AC=6,BD=2,求得OA与OB的长,再由三角形的三边关系,求得x的取值范围,继而求得答案.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴OA=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,OB=$\frac{1}{2}$BD=$\frac{1}{2}$×2=1,
∴2<AB<4,
故选C.
点评 此题考查了平行四边形的性质、三角形的三边关系以及在数轴上表示不等式的解集.注意平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.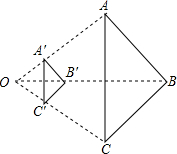 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:9 |
19.下列图案中,可以看作是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,⊙O为△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,D为⊙O上一点,∠ABC=∠ODC=67.5°.
如图,⊙O为△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,D为⊙O上一点,∠ABC=∠ODC=67.5°.
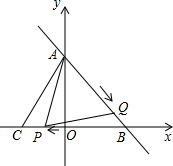 已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0).
已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0). 如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.
如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.