题目内容
15.为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:(1)请由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数;
(2)请由此估算出这个月该时段通过该路口的汽车数量的日平均数;
(3)请根据统计图和以上计算的数据,计算出该路口一年(12个月365天)日过汽车数量超过200辆的概率.
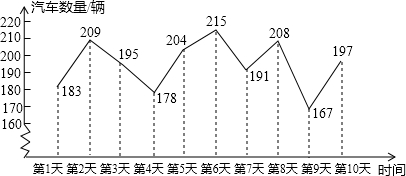
分析 (1)先由折线统计图得出10天中在同一时段通过该路口的汽车数量超过200辆的天数,求出其频率,再利用样本估计总体的思想即可求解;
(2)根据平均数的计算方法计算可得;
(3)由(1)中知一个月通过该路口的汽车数量超过200辆的天数约有12天,可估测一年中该路口的汽车数量超过200辆的天数,根据概率公式计算可得.
解答 解:(1)由图可知,10天中在同一时段通过该路口的汽车数量超过200辆的有4天,频率为:$\frac{4}{10}$=0.4,
所以估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为:30×0.4=12(天);
(2)这个月该时段通过该路口的汽车数量的日平均数为:$\frac{183+209+195+178+204+215+191+208+167+197}{10}$=194.7(辆/天);
(3)由(1)知,一个月该时段通过该路口的汽车数量超过200辆的有12天,
∴该路口一年(12个月365天)日过汽车数量超过200辆的概率为$\frac{12×12}{365}$=$\frac{144}{365}$.
点评 本题考查了折线统计图及用样本估计总体的思想及概率公式的运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
16.下列说法正确的是( )
| A. | “任意画一个三角形,其内角和为360°”是随机事件 | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投十次可投中6次 | |
| C. | 抽样调查选取样本时,所选样本可按自己的喜好选取 | |
| D. | 检测某城市的空气质量,采用抽样调查法 |
6.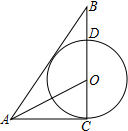 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
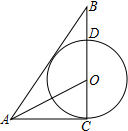 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}π$ | D. | $\frac{16}{9}π$ |
4.下列运算中,计算正确的是( )
| A. | x2y÷y=x2 | B. | (2x2)3=6x5 | C. | (-π)0=0 | D. | a6÷a3=a2 |
5. 如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
 如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )| A. | (1,$\frac{5}{2}$) | B. | ($\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\sqrt{5}$,2$\sqrt{5}$) | D. | ($\sqrt{3}$,2$\sqrt{3}$) |




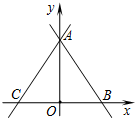 如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.
如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.