题目内容
2.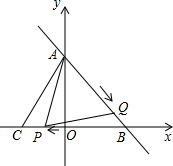 已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0).
已知:如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,点C的坐标是(-2,0).(1)请直接写出AB的长度;
(2)现有一动点P从B出发由B向C运动,另一动点Q从A出发由A向B运动,两点同时出发,速度均为每秒1个单位,当P运动到C时停止.设从出发起运动了t秒,△APQ的面积为S.
①试求S与t的函数关系式,并写出自变量t的取值范围?
②问当t为何值时,△APQ是一个以AP为腰的等腰三角形?
分析 (1)先求出A、B坐标,关键勾股定理即可解决问题.
(2)①如图,作QM⊥y轴于点吗,QN⊥x轴于N,由△AMQ∽△AOB,得$\frac{AQ}{AB}$=$\frac{QM}{OB}$=$\frac{AM}{AO}$求出AM,MQ,根据S=S△ABC-S△ACP-S△PQB即可解决问题.
②i)AP=AQ时,根据AP2=AQ2,列出方程解决问题.
ii)当PA=PQ时,根据PA2=PQ2,列出方程解决问题.
解答 解:(1)∵直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A、B,
∴A(3,0),B(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5.
(2)①如图,作QM⊥y轴于点吗,QN⊥x轴于N,
∵QM∥OB,
∴△AMQ∽△AOB,
∴$\frac{AQ}{AB}$=$\frac{QM}{OB}$=$\frac{AM}{AO}$,即$\frac{t}{5}$=$\frac{QM}{3}$=$\frac{AM}{4}$,
∴QM=$\frac{3}{5}$t,AM=$\frac{4}{5}$t,OM=4-$\frac{4}{5}$t,CP=5-t,
∵四边形ONQM是矩形,
∴QN=OM,MQ=ON,
∴S△ACP=$\frac{1}{2}$CP•AO=10-2t,S△QPB=$\frac{1}{2}$PB•QN=2t-$\frac{2}{5}$t2,
∴S=S△ABC-S△ACP-S△PQB=$\frac{2}{5}$t2(0<t≤5).
②在RT△APO中,AP2=PO2+AO2=(t-3)2+42,
由①可知NB=3-$\frac{3}{5}$t,
在RT△PQN中,PN=PB-BN=$\frac{8}{5}$t-3,
∴PQ2=PN2+QN2=($\frac{8}{5}$t-3)2+(4-$\frac{4}{5}$t)2,
i)当AP=AQ时,AP2=AQ2,即(t-3)2+42=t2,解得t=$\frac{25}{6}$,
ii)当PA=PQ时,PA2=PQ2,即(t-3)2+42=($\frac{8}{5}$t-3)2+(4-$\frac{4}{5}$t)2,解得t=$\frac{50}{11}$或0(舍弃).
综上所述t=$\frac{25}{6}$或$\frac{50}{11}$时,△APQ是一个以AP为腰的等腰三角形.
点评 本题考查一次函数综合题、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会利用分割法求面积,学会分类讨论,学会把问题转化为方程解决问题,不能漏解,属于中考压轴题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| 医疗费用范围 | 报销比例标准 |
| 不超过800元 | 不予报销 |
| 超过800元且不超过3000元的部分 | 50% |
| 超过3000元且不超过5000元的部分 | 60% |
| 超过5000元的部分 | 70% |
 如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )
如图,在Rt△ABC中,∠B=90°,cosA=$\frac{12}{13}$,则tanA=( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{12}$ | C. | $\frac{12}{13}$ | D. | $\frac{5}{12}$ |
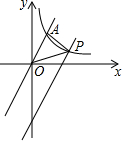 如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.
如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.



