题目内容
11.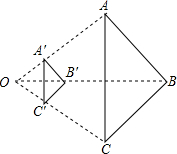 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:9 |
分析 先求出位似比,根据位似比等于相似比,再由相似三角形的面积比等于相似比的平方即可.
解答 解:∵OB=3OB′,
∴$\frac{OB′}{OB}=\frac{1}{3}$,
∵以点O为位似中心,将△ABC缩小后得到△A′B′C′,
∴△A′B′C′∽△ABC,
∴$\frac{A′B′}{AB}=\frac{OB′}{OB}$=$\frac{1}{3}$.
∴$\frac{{S}_{△A′B′C′}}{{S}_{△ABC}}=({\frac{A′B′}{AB})}^{2}$=$\frac{1}{9}$,
故选D
点评 此题是位似变换,主要考查了位似比等于相似比,相似三角形的面积比等于相似比的平方,解本题的关键是掌握位似的性质.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | “任意画一个三角形,其内角和为360°”是随机事件 | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投十次可投中6次 | |
| C. | 抽样调查选取样本时,所选样本可按自己的喜好选取 | |
| D. | 检测某城市的空气质量,采用抽样调查法 |
20.2016的相反数是( )
| A. | -2016 | B. | 2016 | C. | -$\frac{1}{2016}$ | D. | $\frac{1}{2016}$ |
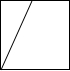
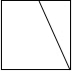
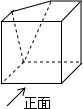 如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )
如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )

 如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.
如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.
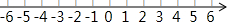 解下列不等式组,并将它的解集在数轴上表示出来.
解下列不等式组,并将它的解集在数轴上表示出来.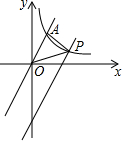 如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.
如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.


