题目内容
1.计算:(1)计算:$\sqrt{3}$tan30°+$\sqrt{2}$cos45°-2sin60°
(2)解方程:(x+1)2=3(x+1)
分析 (1)根据实数的运算顺序,首先计算乘法,然后从左向右依次计算,求出算式$\sqrt{3}$tan30°+$\sqrt{2}$cos45°-2sin60°的值是多少即可.
(2)因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.
解答 解:(1)$\sqrt{3}$tan30°+$\sqrt{2}$cos45°-2sin60°
=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-2×$\frac{\sqrt{3}}{2}$
=1+1-$\sqrt{3}$
=2-$\sqrt{3}$
(2)(x+1)2=3(x+1)
(x+1)2-3(x+1)=0
(x+1)(x+1-3)=0
(x+1)(x-2)=0
∴x+1=0或x-2=0,
解得x=-1或x=2.
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了特殊角的三角函数值,要牢记30°、45°、60°角的各种三角函数值.
(3)此题还考查了因式分解法解一元二次方程,要熟练掌握.

练习册系列答案
相关题目
20.2016的相反数是( )
| A. | -2016 | B. | 2016 | C. | -$\frac{1}{2016}$ | D. | $\frac{1}{2016}$ |
6.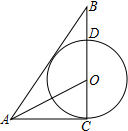 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
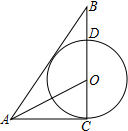 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}π$ | D. | $\frac{16}{9}π$ |
13.某市政府为了增强城镇居民抵御大病风险的能力,积极完善城镇居民医疗保险制度,纳入医疗保险的居民大病住院医疗费用的报销比例标准如下表:
设享受医保的某居民一年的大病住院医疗费用为x元,按上述标准报销的金额为y元.请写出800<x≤3000时,y关于x的函数关系式为y=$\frac{1}{2}$x-400.
| 医疗费用范围 | 报销比例标准 |
| 不超过800元 | 不予报销 |
| 超过800元且不超过3000元的部分 | 50% |
| 超过3000元且不超过5000元的部分 | 60% |
| 超过5000元的部分 | 70% |
 如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.
如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.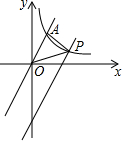 如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.
如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.


