题目内容
9.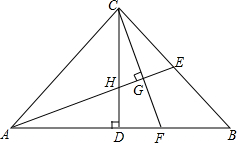 如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H.
如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H.(1)求证:AH=CF;
(2)若BE=2DH,求证:CE=BF.
分析 (1)根据等腰直角三角形的性质得到∠ACD=∠ABC=45°,根据余角的性质得到∠CHG=∠CFD,求得∠AHC=∠BFC,推出△AHC≌△BFC,根据全等三角形的性质即可得到结论;
(2)过D作DM∥BC交AE于M,根据等腰直角三角形的性质得到AD=BD,根据三角形的中位线的性质得到DM=$\frac{1}{2}$BE,求得DM=DH,得到∠DMH=∠DHM,证得CH=CE,由于CH=CF,等量代换即可得到结论.
解答 证明:(1)∵在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,
∴∠ACD=∠ABC=45°,
∵AE⊥CF于点G,
∴∠CHG+∠HCG=∠CFD+∠HCG=90°,
∴∠CHG=∠CFD,
∴∠AHC=∠BFC,
在△AHC与△BCF中,
$\left\{\begin{array}{l}{∠ACH=∠B}\\{∠AHC=∠BFC}\\{AC=BC}\end{array}\right.$,
∴△AHC≌△BFC,
∴AH=CF;
(2)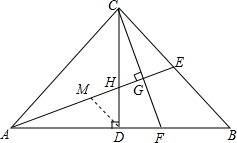 过D作DM∥BC交AE于M,
过D作DM∥BC交AE于M,
∵在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,
∴AD=BD,
∴DM=$\frac{1}{2}$BE,
∵BE=2DH,
∴DM=DH,
∴∠DMH=∠DHM,
∵∠DMH=∠CEH,∠MHD=∠CHE,
∴∠CHE=∠CEH,
∴CH=CE,
∵△AHC≌△BFC,
∴CH=BF,
∴CE=BF.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,平行线的性质,三角形的中位线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
12.某工艺品生产厂为了按时完成订单,对员工采取生产奖励活动,奖励办法以下表计算奖励金额,但是一个月后还是不能按时完成,厂家请工程师改进工艺流程,提高了产量.改进工艺前一月生产A、B两种工艺品共413件,改进工艺后的第一个月生产这两种工艺品共510件,其中A和B的生产量分别比改进工艺前一个月增长25%和20%.
(1)在工艺改进前一个月,员工共获得奖励金额多少元?
(2)如果某车间员工想获得5500元奖金,需要生产多少件工艺品;
(3)改进工艺前一个月,生产的A、B两种工艺品分别为多少件?
| 产量(x件) | 每件奖励金额(元) |
| 0<x≤100 | 10 |
| 100<x≤300 | 20 |
| x>300 | 30 |
(2)如果某车间员工想获得5500元奖金,需要生产多少件工艺品;
(3)改进工艺前一个月,生产的A、B两种工艺品分别为多少件?
14. 如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
 如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
1.若x、y为有理数,下列各式成立的是( )
| A. | (-x)3=x3 | B. | (-x)4=-x4 | C. | x4=-x4 | D. | -x3=(-x)3 |
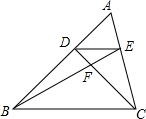 如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.
如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$. 如图,在平面直角坐标系中,四边形OABC各个顶点的坐标分别为O(0,0),A(6,0),B(4,4),C(2,3),求这个四边形OABC的面积.
如图,在平面直角坐标系中,四边形OABC各个顶点的坐标分别为O(0,0),A(6,0),B(4,4),C(2,3),求这个四边形OABC的面积.