题目内容
4. 如图,在平面直角坐标系中,四边形OABC各个顶点的坐标分别为O(0,0),A(6,0),B(4,4),C(2,3),求这个四边形OABC的面积.
如图,在平面直角坐标系中,四边形OABC各个顶点的坐标分别为O(0,0),A(6,0),B(4,4),C(2,3),求这个四边形OABC的面积.
分析 首先将四边形OABC分割成两个三角形和一个梯形,利用点的坐标,求出各个线段的对应长度,进而求出面积.
解答 解:分别过点C、B作CD⊥x轴,BE⊥x轴,垂足分别为D、E,如下图:
∵O(0,0),A(6,0),B(4,4),C(2,3),
∴OD=2,DE=2,AE=2,CD=3,BE=4,
S四边形OABC
=S△OCD+S梯形CDEB+S△ABE
=$\frac{1}{2}$×OD×CD+$\frac{1}{2}$×(CD+BE)×DE+$\frac{1}{2}$×AE×BE
=$\frac{1}{2}$×2×3+$\frac{1}{2}$(3+4)×2+$\frac{1}{2}$×2×4
=3+7+4
=14.
答:四边形OABC的面积为14.
点评 题目考查了直角坐标系中图形面积的求解,解决此类问题关键是将不规则图形分割成可以求解的图形,另外需要注意运算的正确性.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9.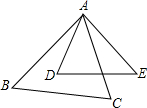 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )| A. | $\frac{AC}{AD}$=$\frac{AB}{AE}$ | B. | $\frac{AC}{AD}$=$\frac{BC}{DE}$ | C. | $\frac{AC}{AD}$=$\frac{AB}{DE}$ | D. | $\frac{AC}{AD}$=$\frac{BC}{AE}$ |
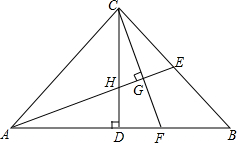 如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H.
如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H. 如图,建立适当的坐标系,写出图中几个关键点的坐标.
如图,建立适当的坐标系,写出图中几个关键点的坐标.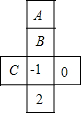 如图所示,这是一个正方体纸盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们在折成正方形后相对的面上的两个数互为相反数,则A+B+C的值是-1.
如图所示,这是一个正方体纸盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们在折成正方形后相对的面上的两个数互为相反数,则A+B+C的值是-1.