题目内容
14.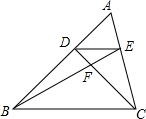 如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.
如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.
分析 由DE∥BC,证得△ADE∽△ABC,根据相似三角形的性质得到$\frac{AE}{AC}=\frac{DE}{BC}$=$\frac{1}{3}$,由于△DEF∽△BCF,根据相似三角形的性质即可得到结论.
解答 解:∵AE=1,CE=2,
∴AC=3,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}=\frac{DE}{BC}$=$\frac{1}{3}$,
∵DE∥BC,
∴△DEF∽△BCF,
∴$\frac{EF}{BF}=\frac{DE}{BC}$=$\frac{1}{3}$,
故答案为:1:3.
点评 本题考查了相似三角形的判定和性质,熟练正确相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.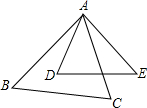 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )| A. | $\frac{AC}{AD}$=$\frac{AB}{AE}$ | B. | $\frac{AC}{AD}$=$\frac{BC}{DE}$ | C. | $\frac{AC}{AD}$=$\frac{AB}{DE}$ | D. | $\frac{AC}{AD}$=$\frac{BC}{AE}$ |
 如图是一个正方体的平面展开图,在这个正方体中相对的面上的数字互为相反数,那么m所表示的数应是3.
如图是一个正方体的平面展开图,在这个正方体中相对的面上的数字互为相反数,那么m所表示的数应是3. 如图是二次函数y=ax2+bx+c的部分图象,在下列四个结论中正确的是①③(写出所有正确结论的序号)
如图是二次函数y=ax2+bx+c的部分图象,在下列四个结论中正确的是①③(写出所有正确结论的序号)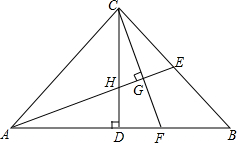 如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H.
如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H.