题目内容
14. 如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据等边三角形性质得出AB=AC,根据三线合一定理得出①正确;求出△BAE≌△CAD,推出BE=DC=BD,∠DAC=∠BAE=30°,求出∠BAE=∠BAD,根据三线合一得出EF=DF.
解答 解:∵△ABC是等边三角形,
∴AB=AC,
∵AD是∠BAC的平分线,
∴AD⊥BC,BD=DC,
∴∠ADC=90°,
∵△ABC和△ADE是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD-∠BAD=∠BAC-∠BAD,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAB=∠DAC}\\{AB=AC}\end{array}\right.$,
∴△BAE≌△CAD(SAS),
∴∠DAC=∠BAE,BE=DC,
∵BD=DC,
∴BE=BD,
∵△ABC是等边三角形,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠DAC=30°,
∴∠BAE=30°,
∵△ADE是等边三角形,
∴∠DAE=60°,
∴∠BAD=30°=∠BAE,
∵AE=AD,
∴EF=DF(三线合一),
∵△BAE≌△CAD,
∴∠ABE=∠C=60°,
∵∠BAC=60°,
∴∠ABE=∠BAC,
∴BE∥AC,
即①②③④都正确,
故选A.
点评 本题考查了全等三角形的性质和判定,等边三角形的性质,等腰三角形的性质的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
20.一元二次方程x2+x+1=0的根的情况为( )
| A. | 有两个相等的实数根 | B. | 没有实根 | ||
| C. | 只有一个实数根 | D. | 有两个不相等的实数根 |
6.点A(-3,5)关于原点的对称点的坐标为( )
| A. | (3,5) | B. | (-3,-5) | C. | (3,-5) | D. | (5,-3) |
3.下列各数中,最大的数是( )
| A. | 0 | B. | -1 | C. | -2 | D. | 1 |
 四边形ABCD在平面直角坐标系中的位置如图所示,若AB⊥AD,AB∥CD,且AB=5,A点坐标为(-2,7),则B点坐标为(3,7).
四边形ABCD在平面直角坐标系中的位置如图所示,若AB⊥AD,AB∥CD,且AB=5,A点坐标为(-2,7),则B点坐标为(3,7).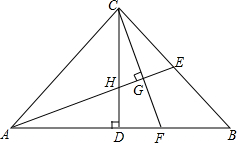 如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H.
如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D、E、F分别为BC,AB上的点.AE⊥CF于点G,交CD于点H.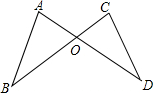 如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.
如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.