题目内容
3.方程|x+3|-|x-1|=x+1的解是x=-5或x=3或x=-1 (直接写出答案).分析 充分利用绝对值的几何意义,采用分类讨论的方法,去掉绝对值再一一计算.
解答 解:(1)当x≤-3时,原方程可化为:-x-3+x-1=x+1,
解得:x=-5;
(2)当x≥1时,原方程可化为:x+3-x+1=x+1,
解得:x=3;
(3)当-3<x<1时,原方程可化为::-x-3-x+1=x+1,
解得:x=-1.
2x+3-1+x=4x-3
综上所述,方程的解为:x=-5或x=3或x=-1.
故答案为:x=-5或x=3或x=-1.
点评 本题主要考查的是含有绝对值符号的一元一次方程的一般计算,难易适中,关键是分类思想的运用.

练习册系列答案
相关题目
8. 如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
 如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )| A. | 12π-16$\sqrt{7}$ | B. | 16π-18$\sqrt{7}$ | C. | 16π-24$\sqrt{7}$ | D. | 16π-12$\sqrt{7}$ |
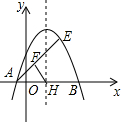 如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).
如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).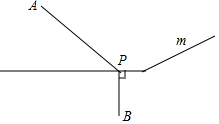 如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.
如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.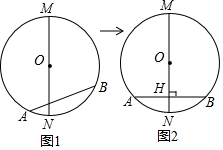
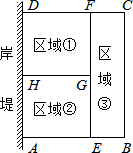 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.