题目内容
13.A、B两地相距600千米,一列慢车从A地开出,每小时行驶80千米,一列快车从B地开出,每小时行驶120千米,两车同时开出.(1)若相向而行,出发后多少小时相遇?
(2)若相背而行,多少小时后,两车相距800千米
(3)若两车同向而行,快车在慢车后面,多少小时后,快车追上慢车?
分析 (1)设出发后x小时两车相遇,根据两地间距=相遇时间×两车速度之和,即可列出关于x的一元一次方程,解之即可得出结论;
(2)设y小时后两车相距800千米,根据行驶时间×两车速度和=两车间距-两地间距,即可列出关于y的一元一次方程,解之即可得出结论;
(3)设出发后z小时快车追上慢车,根据两地间距=相遇时间×两车速度之差,即可列出关于z的一元一次方程,解之即可得出结论.
解答 解:(1)设出发后x小时相遇,
根据题意,可得(80+120)x=600,
解得x=3.
答:若相向而行,出发后3小时相遇;
(2)设y小时后两车相距800千米,
根据题意,可得(80+120)y=800-600,
解得y=1.
答:若相背而行,1小时后,两车相距800千米;
(3)设z小时后快车追上慢车,
根据题意,可得(120-80)z=600,
解得 z=15.
答:若两车同向而行,快车在慢车后面,15小时后,快车追上慢车.
点评 本题考查了一元一次方程的应用,掌握行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列去括号中,正确的是( )
| A. | a2-(2a-1)=a2-2a-1 | B. | a2+(-2a-3)=a2-2a+3 | ||
| C. | -(a+b)+(c-d)=-a-b-c+d | D. | 3a-[5b-(2c-1)]=3a-5b+2c-1 |
 如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.
如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.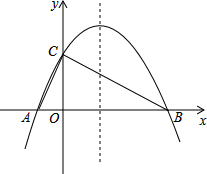 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0). 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,则四边形ABCD的面积为=31,BD的长为2$\sqrt{41}$.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,则四边形ABCD的面积为=31,BD的长为2$\sqrt{41}$.