题目内容
12.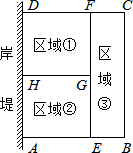 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.(1)求证:AE=2BE;
(2)求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)x为何值时,y有最大值?最大值是多少?
分析 (1)根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE;
(2)设BE=a,则有AE=2a,表示出a与2a,进而表示出y与x的关系式,并求出x的范围即可;
(3)利用二次函数的性质求出y的最大值,以及此时x的值即可.
解答 解:(1)∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
又∵EF是公共边,
∴AE=2BE;
(2)设BE=a,则AE=2a,
∴8a+2x=80,
∴a=$\frac{80-2x}{8}$,AB=3a,
∴y=3ax=3•$\frac{80-2x}{8}$•x=-$\frac{3}{4}$x2+30x,
∵a=-x+40>0,
∴x<40,
∴0<x<40
(3)∵y=-$\frac{3}{4}$x2+30x=-$\frac{3}{4}$(x-20)2+300(0<x<40),且二次项系数为-$\frac{3}{4}$<0,
∴当x=20时,y有最大值,最大值为300平方米.
点评 此题考查了二次函数的应用,以及列代数式,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.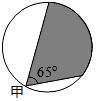 如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
 如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )| A. | 25° | B. | 65° | C. | 115° | D. | 130° |
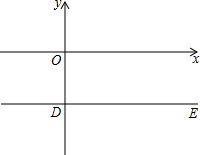 已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.
已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A. 如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长.
如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长. 如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E.
如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E. 如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.
如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.