题目内容
7.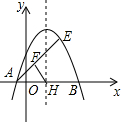 如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).
如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴的交于点是H,点F是AE中点,连接FH.求线段FH的长;
(3)P为直线AE上方抛物线上的点.当△AEP的面积最大时.求P点的坐标.
分析 (1)把E点坐标代入抛物线解析式可求得m的值,可求得抛物线解析式;
(2)由抛物线解析式可求得A点坐标,则可求得F点坐标,由对称轴可求得H坐标,则可求得FH的长;
(3)由A、E坐标,利用待定系数法可求得直线AE的解析式,过P作PG∥y轴,交直线AE于点G,设出P点坐标,则可表示出G点坐标,从而可表示出PG的长,进一步表示出△APE的面积,利用二次函数的性质可求得其最大值时的点P坐标.
解答 解:
(1)∵y=-(x-1)2+m经过E(2,3),
∴3=-(2-1)2+m,解得m=4,
∴抛物线解析式为y=-(x-1)2+4;
(2)在y=-(x-1)2+4中,令y=0可得-(x-1)2+4=0,解得x=3或x=-1,
∴A(-1,0),
∵F是AE的中点,且E(2,3)
∴F($\frac{1}{2}$,$\frac{3}{2}$),
由抛物线解析式可求得抛物线对称轴为x=1,
∴H(1,0),
∴FH=$\sqrt{(1-\frac{1}{2})^{2}+(0-\frac{3}{2})^{2}}$=$\frac{\sqrt{10}}{2}$;
(3)如图,过P作PG∥y轴,交直线AE于点G,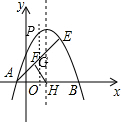
设直线AE解析式为y=kx+b,
∴$\left\{\begin{array}{l}{2k+b=3}\\{-k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线AE解析式为y=x+1,
∵P为直线AE上方抛物线上的点,
∴设P(t,-(t-1)2+4),则G(t,t+1),
∴PG=-(t-1)2+4-(t+1)=-t2+t+2=-(t-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴S△PAE=$\frac{1}{2}$PG•[3-(-1)]=2PG=-2(t-$\frac{1}{2}$)2+$\frac{9}{2}$,
∵-2<0,
∴当t=$\frac{1}{2}$时,S△PAE有最大值,此时P点坐标为($\frac{1}{2}$,$\frac{15}{4}$).
点评 本题为二次函数的综合应用,涉及待定系数法、一元二次方程、勾股定理、中点的定义、三角形的面积、二次函数的性质及方程思想等知识点.在(1)中注意待定系数法的应用,在(2)中利用中点求得F点的坐标是解题的关键,在(3)中用P点的坐标表示出△PAE的面积是解题的关键.本题考查知识点较多,综合性较强,难度适中.

 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案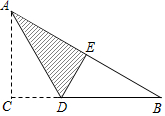 如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )| A. | x2=(8-x)2+62 | B. | x2=(8-x)2+42 | C. | x=8-x+4 | D. | x2=62+82 |


 如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.
如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高. 如图,AB为半圆O的直径,C为半圆上一点,∠AOC=60°,点P在AB的延长线上,且PB=BO=3cm.连接PC交半圆于点D,过P作PE⊥PA交AD的延长线于点E,求PE长.
如图,AB为半圆O的直径,C为半圆上一点,∠AOC=60°,点P在AB的延长线上,且PB=BO=3cm.连接PC交半圆于点D,过P作PE⊥PA交AD的延长线于点E,求PE长. 已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.
已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.