题目内容
15．在进行垂径定理的证明教学中，老师设计了如下活动：先让同学们在圆中作了一条直径MN，然后任意作了一条弦（非直径），如图1，接下来老师提出问题：在保证弦AB长度不变的情况下，如何能找到它的中点？在同学们思考作图验证后，小华说了自己的一种想法：只要将弦AB与直径MN保持垂直关系，如图2，它们的交点就是弦AB的中点．请你说出小华此想法的依据是等腰三角形三线合一定理．
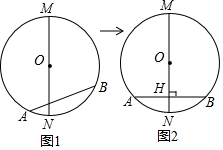
分析 连接OA、OB，则△OAB是等腰三角形，依据等腰三角形的性质判断．
解答 解：连接OA、OB，则△OAB是等腰三角形，当MB过AB的中点时，一定有MN⊥AB，依据三线合一定理可得．
故答案是：等腰三角形三线合一定理．
点评 本题考查了垂径定理，正确转化为等腰三角形的性质解决问题是关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，AB为半圆O的直径，C为半圆上一点，∠AOC=60°，点P在AB的延长线上，且PB=BO=3cm．连接PC交半圆于点D，过P作PE⊥PA交AD的延长线于点E，求PE长．
如图，△ABC为等边三角形，D，E两点分别在AB，AC边上，DB=AE，BE，CD相交于点F，BH⊥CD于点H，若EF=1，CD=9，求HF的长．
如图，A，B是直线l上的两点，AB=4厘米，过l外一点C作CD∥l，射线BC与l所组成的锐角为60°，线段BC=2厘米，动点P、Q分别从B、C同时出发，P以1厘米/秒的速度，沿由B向C的方向运动；Q以2厘米/秒的速度，沿由C向D的方向运动，设P、Q运动的时间为t秒，当t＞2时，PA交CD于点E．
如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=10，DA=5$\sqrt{5}$，则四边形ABCD的面积为=31，BD的长为2$\sqrt{41}$．