题目内容
10.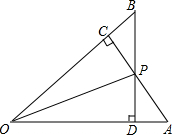 已知,如图,AC⊥OB,BD⊥OA,垂足分别为C,D,OC=OD,AC与BD相交于点P,求证:PC=PD.
已知,如图,AC⊥OB,BD⊥OA,垂足分别为C,D,OC=OD,AC与BD相交于点P,求证:PC=PD.
分析 根据HL证明Rt△OCP≌Rt△ODP可得结论.
解答 证明:∵AC⊥OB,BD⊥OA,
∴∠ODP=∠OCP=90°,
在Rt△OCP和Rt△ODP中,
∵$\left\{\begin{array}{l}{OP=OP}\\{OC=OD}\end{array}\right.$,
∴Rt△OCP≌Rt△ODP(HL),
∴PC=PD.
点评 本题考查了直角三角形的全等判定,比较简单,找到证明哪两个三角形全等是关键.

练习册系列答案
相关题目
15.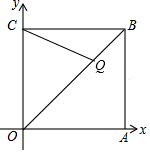 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
19. 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )| A. | 的 | B. | 中 | C. | 国 | D. | 梦 |
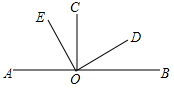 如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)
如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)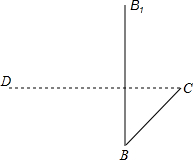 (1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);
(1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);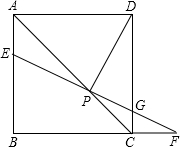 已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.
已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.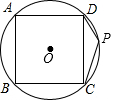 如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.
如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.