题目内容
20.已知,△ABC的三边为9,7,6,与△ABC相似的△DEF的最小边为18,则另两边为27,21.分析 由于△DEF与△ABC相似,因此它们各对应边的比都相等,可据此求出△DEF的另两边长.
解答 解:设△DEF的另两边长各是x,y,
根据相似三角形的对应边的比相等,可得:
18:x:y=6:7:9,
解得:x=21,y=27,
因此△DEF的另两边长各是21和27.
故答案为27,21.
点评 本题主要考查了相似三角形的性质,掌握相似三角形的对应边成比例是解题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
5.下列从左到右变形正确的是( )
| A. | -$\frac{x+1}{x-y}$=$\frac{-x+1}{x-y}$ | B. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a-b}{a+b}$=$\frac{b-a}{b+a}$ |
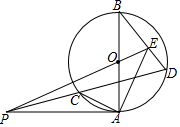 如图,AB为⊙O直径,PA切⊙O于A,PCD为⊙O一条割线,PO交BD于E,证明:AC⊥AE.
如图,AB为⊙O直径,PA切⊙O于A,PCD为⊙O一条割线,PO交BD于E,证明:AC⊥AE.
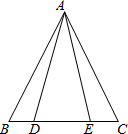 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.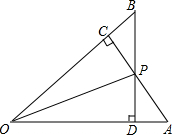 已知,如图,AC⊥OB,BD⊥OA,垂足分别为C,D,OC=OD,AC与BD相交于点P,求证:PC=PD.
已知,如图,AC⊥OB,BD⊥OA,垂足分别为C,D,OC=OD,AC与BD相交于点P,求证:PC=PD.