题目内容
4. 如图是由相同边长的正三角形,正方形,正六边形组成的镶嵌图,若外面这一圈阴影部分面积比中间这个正六边形面积大12cm2,则这些正多边形的边长是$\sqrt{2}$cm.
如图是由相同边长的正三角形,正方形,正六边形组成的镶嵌图,若外面这一圈阴影部分面积比中间这个正六边形面积大12cm2,则这些正多边形的边长是$\sqrt{2}$cm.
分析 先设出相同边长的正三角形,正方形,正六边形为x,根据题意列方程得:6x2+6×$\frac{\sqrt{3}}{4}$x2-4×$\frac{\sqrt{3}}{4}$x2=12,解方程即可.
解答 解:设相同边长的正三角形,正方形,正六边形为x,
根据题意列方程得:6x2+6×$\frac{\sqrt{3}}{4}$x2-4×$\frac{\sqrt{3}}{4}$x2=12,
∴x=$\sqrt{2}$或x=-$\sqrt{2}$(舍)
故答案为:$\sqrt{2}$
点评 此题是正多边形和圆,主要考查了多边形的面积的计算方法,解本题的关键是求出正六边形的面积.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
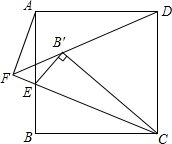 如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为$\frac{3\sqrt{10}}{5}$.
如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为$\frac{3\sqrt{10}}{5}$. △ABC中,∠A=30°,∠B=45°,AC=4,求AB的长?
△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长?