题目内容
6.我们知道完全平方式(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,两式相加得(a+b)2+(a-b)2=2a2+2b2,即a2+b2=$\frac{1}{2}$[(a+b)2+(a-b)2].两式相减得(a+b)2-(a-b)2=4ab,即ab=$\frac{1}{4}$[(a+b)2-(a-b)2],请利用以上性质完全下列问题:已知(x+y)2=6,(x-y)2=2,试求:(1)x2+y2的值
(2)xy的值.
分析 (1)将(x+y)2=6、(x-y)2=2代入x2+y2=$\frac{1}{2}$[(x+y)2+(x-y)2]可得;
(2)将(x+y)2=6、(x-y)2=2代入xy=$\frac{1}{4}$[(x+y)2-(x-y)2]可得.
解答 解:(1)∵(x+y)2=6,(x-y)2=2,
∴x2+y2=$\frac{1}{2}$[(x+y)2+(x-y)2]=$\frac{1}{2}$×(6+2)=4.
(2)xy=$\frac{1}{4}$[(x+y)2-(x-y)2]=$\frac{1}{4}$×(6-2)=1.
点评 本题主要考查完全平方公式,熟练掌握题目中的有关性质是解题的关键.

练习册系列答案
相关题目
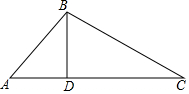 如图,在△ABC中,∠ABC=120°,BD是AC边上的高,若AB+AD=DC,则∠C等于20°.
如图,在△ABC中,∠ABC=120°,BD是AC边上的高,若AB+AD=DC,则∠C等于20°.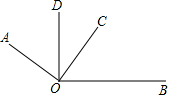 如图,∠AOC与∠BOD都是直角.
如图,∠AOC与∠BOD都是直角. 如图是由相同边长的正三角形,正方形,正六边形组成的镶嵌图,若外面这一圈阴影部分面积比中间这个正六边形面积大12cm2,则这些正多边形的边长是$\sqrt{2}$cm.
如图是由相同边长的正三角形,正方形,正六边形组成的镶嵌图,若外面这一圈阴影部分面积比中间这个正六边形面积大12cm2,则这些正多边形的边长是$\sqrt{2}$cm.