题目内容
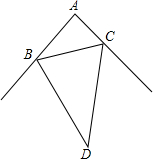 如图,在△ABC中,∠A=90°,∠D是∠ABC和∠ACB的外角平分线的夹角,求∠D的度数.
如图,在△ABC中,∠A=90°,∠D是∠ABC和∠ACB的外角平分线的夹角,求∠D的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据题意求出∠ABC+∠ACB=90°,结合角平分线的定义及三角形的外角定理,求出∠DBC+∠DCB的值,进而求出∠D的值.
解答:解:设∠ABC=x,∠ACB=y;
∵∠A=90°,∴x+y=90°
∵BD,CD分别为△ABC的外角平分线,
∴∠DBC+∠DCB=
+
=
故∠D=180°-
=180°-90°-
=90°-45°=45°
即∠D=45°
∵∠A=90°,∴x+y=90°
∵BD,CD分别为△ABC的外角平分线,
∴∠DBC+∠DCB=
| 90°+y |
| 2 |
| 90°+x |
| 2 |
| 180°+x+y |
| 2 |
故∠D=180°-
| 180°+x+y |
| 2 |
| x+y |
| 2 |
=90°-45°=45°
即∠D=45°
点评:命题考查了三角形的内角和定理、外角定理及其应用问题;解题的关键是充分利用∠ABC+∠ACB=90°为定值这一重要结论,灵活运用内角和定理来解题.

练习册系列答案
相关题目
方程(1-x)2=2的根是( )
| A、-1、3 | ||||
| B、1、-3 | ||||
C、1-
| ||||
D、
|
⊙O1与⊙O2半径分别为4和1,圆心距为2,作⊙O2的切线,被⊙O1所截的最短弦长为( )
| A、10 | ||
| B、8 | ||
C、2
| ||
D、2
|
 △ABC≌△ADE,若∠BAE=130°,∠BAD=44°,则∠BAC=
△ABC≌△ADE,若∠BAE=130°,∠BAD=44°,则∠BAC=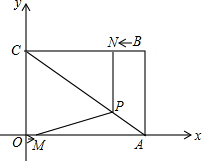 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了t秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了t秒.