题目内容
如图(1),MN是⊙O的直径,弦AB、CD相交于MN上一点P,且PD=PB.

(1)求证:AB=CD;
(2)如图(2)若AB、CD相交于MN延长线上一点P,其他条件不变,则AB=CD还成立吗?请说明理由.

(1)求证:AB=CD;
(2)如图(2)若AB、CD相交于MN延长线上一点P,其他条件不变,则AB=CD还成立吗?请说明理由.
考点:圆周角定理,圆心角、弧、弦的关系
专题:
分析:(1)先由相交弦定理得出PA•PB=PC•PD,而PD=PB,所以PA=PC,然后根据等式的性质即可证明AB=CD;
(2)先由切割线定理得出PB•PA=PD•PC,而PD=PB,所以PA=PC,然后根据等式的性质即可得出AB=CD.
(2)先由切割线定理得出PB•PA=PD•PC,而PD=PB,所以PA=PC,然后根据等式的性质即可得出AB=CD.
解答:(1)证明:∵MN是⊙O的直径,弦AB、CD相交于MN上一点P,
∴PA•PB=PC•PD,
∵PD=PB,
∴PA=PC,
∴PA+PB=PC+PD,
即AB=CD;
(2)解:AB=CD还成立.理由如下:
∵AB、CD相交于NM延长线上一点P,
∴PB•PA=PD•PC,
∵PD=PB,
∴PA=PC,
∴PA-PB=PC-PD,
即AB=CD.
∴PA•PB=PC•PD,
∵PD=PB,
∴PA=PC,
∴PA+PB=PC+PD,
即AB=CD;
(2)解:AB=CD还成立.理由如下:
∵AB、CD相交于NM延长线上一点P,
∴PB•PA=PD•PC,
∵PD=PB,
∴PA=PC,
∴PA-PB=PC-PD,
即AB=CD.
点评:本题考查了相交弦定理,切割线定理以及等式的性质,得出PA=PC是解题的关键.

练习册系列答案
相关题目
 如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则CD的长为( )
如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则CD的长为( )| A、6cm | B、4.8cm |
| C、2.4cm | D、1.2cm |
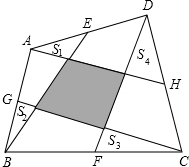 如图,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,图中阴影部分的面积为20平方厘米,求图中四个小三角形的面积和.
如图,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,图中阴影部分的面积为20平方厘米,求图中四个小三角形的面积和.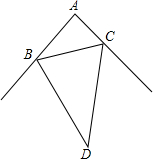 如图,在△ABC中,∠A=90°,∠D是∠ABC和∠ACB的外角平分线的夹角,求∠D的度数.
如图,在△ABC中,∠A=90°,∠D是∠ABC和∠ACB的外角平分线的夹角,求∠D的度数.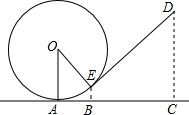 如图是小朋友玩的“滚铁环“游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A.若⊙O的半径为25cm,cos∠AOE=
如图是小朋友玩的“滚铁环“游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A.若⊙O的半径为25cm,cos∠AOE=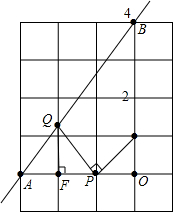 如图,直线y=
如图,直线y=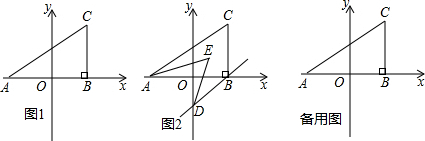
 如图所示,已知△ABC是等边三角形,∠B、∠C的平分线相交于O,OD∥AB,OE∥AC.试说明:BD=DE=EC.
如图所示,已知△ABC是等边三角形,∠B、∠C的平分线相交于O,OD∥AB,OE∥AC.试说明:BD=DE=EC.