题目内容
已知(a-1)x2-(a2+1)x+a2+a=0的根是正整数,求a的整数值.
考点:根与系数的关系,一元一次方程的解
专题:计算题
分析:分类讨论:当a-1=0,解a=1,原方程变形一元一次方程,解得x=1;当a-1≠0,利用因式分解法解方程得到x1=
,x2=a,由于x1=
=
=1+
,根据整数的整除性易得a=-1,0,2,3,然后综合两种情况即可.
| a+1 |
| a-1 |
| a+1 |
| a-1 |
| a-1+2 |
| a-1 |
| 2 |
| a-1 |
解答:解:当a-1=0,解a=1,原方程变形为-2x+2=0,解得x=1;
当a-1≠0,即a≠1时,[(a-1)x-(a+1)](x-a)=0,解得x1=
,x2=a,
因为x1=
=
=1+
,
而a为整数,x1也为整数,
所以a-1=±1,±2,
所以a=-1,0,2,3,
综上所述,整数a的值为-1,0,1,2,3.
当a-1≠0,即a≠1时,[(a-1)x-(a+1)](x-a)=0,解得x1=
| a+1 |
| a-1 |
因为x1=
| a+1 |
| a-1 |
| a-1+2 |
| a-1 |
| 2 |
| a-1 |
而a为整数,x1也为整数,
所以a-1=±1,±2,
所以a=-1,0,2,3,
综上所述,整数a的值为-1,0,1,2,3.
点评:本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了解一元二次方程.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
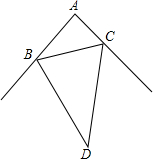 如图,在△ABC中,∠A=90°,∠D是∠ABC和∠ACB的外角平分线的夹角,求∠D的度数.
如图,在△ABC中,∠A=90°,∠D是∠ABC和∠ACB的外角平分线的夹角,求∠D的度数.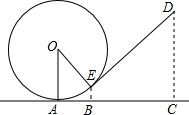 如图是小朋友玩的“滚铁环“游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A.若⊙O的半径为25cm,cos∠AOE=
如图是小朋友玩的“滚铁环“游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A.若⊙O的半径为25cm,cos∠AOE=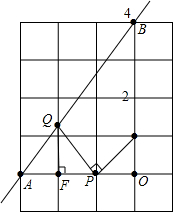 如图,直线y=
如图,直线y= 如图所示,已知△ABC是等边三角形,∠B、∠C的平分线相交于O,OD∥AB,OE∥AC.试说明:BD=DE=EC.
如图所示,已知△ABC是等边三角形,∠B、∠C的平分线相交于O,OD∥AB,OE∥AC.试说明:BD=DE=EC.