题目内容
⊙O1与⊙O2半径分别为4和1，圆心距为2，作⊙O2的切线，被⊙O1所截的最短弦长为（ ）
| A、10 | ||
| B、8 | ||
C、2
| ||
D、2
|
考点：切线的性质,垂径定理,圆与圆的位置关系
专题：
分析：先画出图形，求得O1C的长，⊙O2的切线中被⊙O1所截的最短弦为垂直于O1O2的切线，再根据勾股定理求得AC的长，最后由垂径定理即可得解．
解答：
解：O1C=2+1=3，
在直角△AO1C中，AC=
=
=
，
则AB=2AC=2
．
故选：C．
解：O1C=2+1=3，在直角△AO1C中，AC=
| O1A2-O1C2 |
| 42-32 |
| 7 |
则AB=2AC=2
| 7 |
故选：C．
点评：本题考查了切线的性质以及垂径定理，得出，⊙O2的切线中被⊙O1所截的最短弦为垂直于O1O2的切线是解题的关键．
练习册系列答案
相关题目
用配方法解关于x的一元二次方程x2-2x-m=0，配方后得到的方程为（ ）
| A、（x-1）2=m-1 |
| B、（x-1）2=m+1 |
| C、（x-1）2=1-m |
| D、（x-1）2=m2-1 |
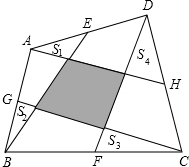如图，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，图中阴影部分的面积为20平方厘米，求图中四个小三角形的面积和．
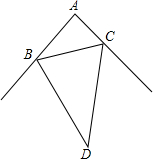如图，在△ABC中，∠A=90°，∠D是∠ABC和∠ACB的外角平分线的夹角，求∠D的度数．
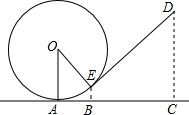如图是小朋友玩的“滚铁环“游戏的示意图，⊙O向前滚动时，铁棒DE保持与OE垂直．⊙O与地面接触点为A．若⊙O的半径为25cm，cos∠AOE=