题目内容
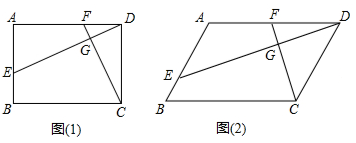
20.已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.(1)如图1,若四边形ABCD是矩形,且DE⊥CF.求证:$\frac{DE}{CF}$=$\frac{AD}{CD}$;
(2)如图2,若四边形ABCD是平行四边形,试探究:当∠B+∠EGC=180°时,求证:$\frac{DE}{CF}$=$\frac{AD}{CD}$.
分析 (1)根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;
(2)证△DFG∽△DEA,得出对应边成比例,证△CGD∽△CDF,得出对应边成比例,即可得出答案;
解答 (1)证明:∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵CF⊥DE,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
∵∠A=∠CDF,
∴△AED∽△DFC,
∴$\frac{DE}{CF}$=$\frac{AD}{CD}$;
(2)证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠B+∠A=180°,
∵∠B+∠EGC=180°
∴∠A=∠EGC=∠FGD,
∵∠FDG=∠EDA,
∴△DFG∽△DEA,
∴$\frac{DE}{AD}=\frac{DF}{DG}$,
∵∠B=∠ADC,∠B+∠EGC=180°,∠EGC+∠DGC=180°,
∴∠CGD=∠CDF,
∵∠GCD=∠DCF,
∴△CGD∽△CDF,
∴$\frac{DF}{DG}=\frac{CF}{CD}$,
∴$\frac{DE}{AD}=\frac{CF}{CD}$,
∴$\frac{DE}{CF}$=$\frac{AD}{CD}$.
点评 本题考查了矩形性质和判定,勾股定理,平行四边形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定的应用,主要考查学生综合运用性质和定理进行推理的能力,题目比较好.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
6.下列四个点中,有三个点在同一反比例函数y=$\frac{k}{x}$的图象上,则不在这个函数图象上的点是( )
| A. | (5,1) | B. | (-1,5) | C. | (-3,-$\frac{5}{3}$) | D. | ($\frac{5}{3}$,3) |
7. 如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2$\sqrt{2}$个单位长度到点O2,点A的位置不变,如果以O2为原点,那么点A的坐标可能是( )
如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2$\sqrt{2}$个单位长度到点O2,点A的位置不变,如果以O2为原点,那么点A的坐标可能是( )
 如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2$\sqrt{2}$个单位长度到点O2,点A的位置不变,如果以O2为原点,那么点A的坐标可能是( )
如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2$\sqrt{2}$个单位长度到点O2,点A的位置不变,如果以O2为原点,那么点A的坐标可能是( )| A. | (3,-1) | B. | (1,-3) | C. | (-2,-1) | D. | (2$\sqrt{2}$+1,2$\sqrt{2}$+1) |
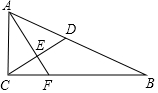 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.

 如图,△ABC中,点D为BC中点,点E为AD中点,点F为CE中点,若S△ABC=10cm2,则S△BEF=2.5cm2.
如图,△ABC中,点D为BC中点,点E为AD中点,点F为CE中点,若S△ABC=10cm2,则S△BEF=2.5cm2. 如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A,B两点,它们的横坐标分别为1和5.
如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A,B两点,它们的横坐标分别为1和5.