题目内容
8.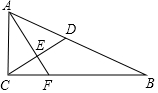 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.
分析 根据勾股定理求出AB,根据等腰三角形的性质得到∠CAF=∠BAF,根据角平分线的性质列出比例式,计算即可.
解答 解:∵∠ACB=90°,AC=5,BC=12,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
∵AD=AC,AF⊥CD,
∴∠CAF=∠BAF,
∴$\frac{CF}{BF}$=$\frac{AC}{AB}$,即$\frac{CF}{12-CF}$=$\frac{5}{13}$,
解得,CF=$\frac{10}{3}$,
故答案为:$\frac{10}{3}$.
点评 本题考查的是勾股定理的应用,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.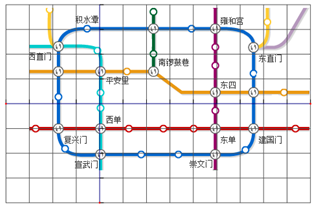 如图,将北京市地铁部分线路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )
如图,将北京市地铁部分线路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )
 如图,将北京市地铁部分线路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )
如图,将北京市地铁部分线路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为( )| A. | (0,5) | B. | (5,0) | C. | (0,-5) | D. | (-5,0) |
17.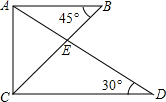 将一副三角尺如图所示叠放在一起,则$\frac{BE}{EC}$的值是( )
将一副三角尺如图所示叠放在一起,则$\frac{BE}{EC}$的值是( )
 将一副三角尺如图所示叠放在一起,则$\frac{BE}{EC}$的值是( )
将一副三角尺如图所示叠放在一起,则$\frac{BE}{EC}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{4}$ |
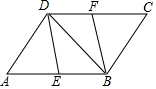 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点. 如图,在△ABC中,∠ACB=90°,CD⊥AB于D点,AB=5,CD=2,则△ABC的周长是3$\sqrt{5}$+5.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D点,AB=5,CD=2,则△ABC的周长是3$\sqrt{5}$+5.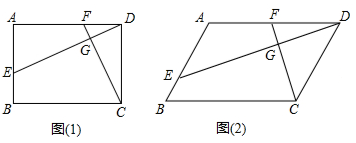
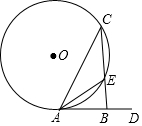 如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE=2.
如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE=2.