Question

5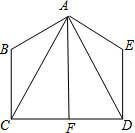．已知，如图，AB=AE，∠B=∠E，BC=ED，∠CAF=∠DAF．求证：AF⊥CD．

Answer 1

分析 利用SAS得到三角形ABC与三角形AED全等，利用全等三角形对应边相等得到AC=AD，再由已知角相等，利用三线合一性质判断即可得证．

解答 证明：在△ABC与△AED中，
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$，
∴△ABC≌△AED（SAS），
∴AC=AD，
∵∠CAF=∠DAF，即AF为∠CAD的平分线，
∴AF⊥CD．

点评 此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．