题目内容
10.下列多边形一定相似的是( )| A. | 两个平行四边形 | B. | 两个菱形 | C. | 两个矩形 | D. | 两个正方形 |
分析 利用相似多边形的对应边的比相等,对应角相等分析.
解答 解:要判断两个多边形是否相似,需要看对应角是否相等,对应边的比是否相等.
矩形、菱形、平行四边形都属于形状不唯一确定的图形,即对应角、对应边的比不一定相等,故不一定相似,A、B、C错误;
而两个正方形,对应角都是90°,对应边的比也都相当,故一定相似,D正确.
故选D
点评 本题考查相似多边形的识别.判定两个图形相似的依据是:对应边的比相等,对应角相等.两个条件必须同时具备.

练习册系列答案
相关题目
18.三角形中,最大的内角不能小于( )
| A. | 60° | B. | 30° | C. | 90° | D. | 45° |
2.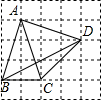 如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
 如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{5}}{5}$ |
19.下列说法正确的是( )
| A. | 8的立方根是±2 | B. | -1不存在立方根 | ||
| C. | 2的算术平方根是$±\sqrt{2}$ | D. | -25不存在平方根 |
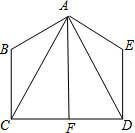 已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD.
已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD. 如图所示的图形是由7个完全相同的小正方体组成的立体图形,则下面四个平面图形中,从三个方向看不能得到的图形是( )
如图所示的图形是由7个完全相同的小正方体组成的立体图形,则下面四个平面图形中,从三个方向看不能得到的图形是( )


