题目内容
13.已知$\frac{b+c+d}{a}=\frac{a+c+d}{b}=\frac{a+b+d}{c}=\frac{a+b+c}{d}$=k,则k=3或-1.分析 分两种情况讨论,当a+b+c+d=0,得到a+b+c=-d,求得k=-1;当a+b+c+d≠0,根据比例的性质得到$\frac{3(a+b+c+d)}{a+b+c+d}$=k,求得k=3.
解答 解:当a+b+c+d=0,
∴a+b+c=-d,∴k=-1;
当a+b+c+d≠0,
∵$\frac{b+c+d}{a}=\frac{a+c+d}{b}=\frac{a+b+d}{c}=\frac{a+b+c}{d}$=k,
∴$\frac{3(a+b+c+d)}{a+b+c+d}$=k,
∴k=3,
∴k=3或-1,
故答案为:3或-1.
点评 本题考查了比例的性质,熟记比例的性质是解题的关键.

练习册系列答案
相关题目
8.如图所示图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.三角形中,最大的内角不能小于( )
| A. | 60° | B. | 30° | C. | 90° | D. | 45° |
2.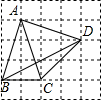 如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
 如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{5}}{5}$ |
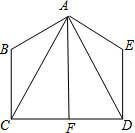 已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD.
已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD.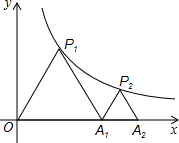 如图,P1、P2是反比例函数y=$\frac{k}{x}$(k>0)在第一象限图象上的两个点,点A1坐标为(4,0),若△P1OA1与△P2A1A2均为等边三角形,则点A2的横坐标为4$\sqrt{2}$.
如图,P1、P2是反比例函数y=$\frac{k}{x}$(k>0)在第一象限图象上的两个点,点A1坐标为(4,0),若△P1OA1与△P2A1A2均为等边三角形,则点A2的横坐标为4$\sqrt{2}$.