题目内容
20.计算:(1)$\frac{z}{{3{x^2}y}}-\frac{y}{{2{x^2}z}}+\frac{x}{{6{y^2}{z^2}}}$
(2)$\frac{x-2}{{{x^2}-1}}÷\frac{2x+2}{{{x^2}+2x+1}}+\frac{1}{x-1}$.
分析 (1)原式通分并利用同分母分式的加减法则计算即可得到结果;
(2)原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算即可得到结果.
解答 解:(1)原式=$\frac{2y{z}^{3}-3{y}^{3}z+{x}^{3}}{6{x}^{2}{y}^{2}{z}^{2}}$;
(2)原式=$\frac{x-2}{(x+1)(x-1)}$•$\frac{(x+1)^{2}}{2(x+1)}$+$\frac{1}{x-1}$=$\frac{x-2}{2(x-1)}$+$\frac{2}{2(x-1)}$=$\frac{x}{2(x-1)}$.
点评 此题考查了分式混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.如图所示图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.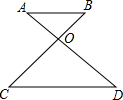 如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
 如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{9}$ | D. | $\frac{4}{3}$ |
9.抛物线y=-3(x+1)2-4的开口方向和顶点坐标分别是( )
| A. | 向下,(1,4) | B. | 向上,(1,4) | C. | 向下,(-1,-4) | D. | 向上,(-1,-4) |
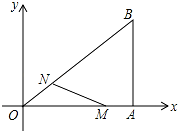 如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题: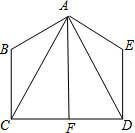 已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD.
已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD.