题目内容
17. 已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.求证:△ABD∽△CBA.
已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.求证:△ABD∽△CBA.
分析 在△ABD与△CBA中,有∠B=∠B,根据已知边的条件,只需证明夹此角的两边对应成比例即可.
解答 证明:∵AB=2,BC=4,BD=1,
∴$\frac{AB}{BC}=\frac{BD}{AB}$,
∵∠B=∠B,
∴△ABD∽△CBA.
点评 本题主要考查了相似三角形的判定及性质;熟记两边成比例且夹角相等的两个三角形相似是解决问题的关键.

练习册系列答案
相关题目
7.两数相加,和比一个加数大,比另一个加数小,则这两个加数( )
| A. | 有一个是0 | B. | 都是正数 | ||
| C. | 都是负数 | D. | 一个是正数,一个是负数 |
8.如图所示图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.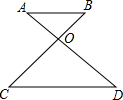 如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
 如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{9}$ | D. | $\frac{4}{3}$ |
2.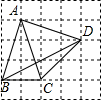 如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
 如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{5}}{5}$ |
9.抛物线y=-3(x+1)2-4的开口方向和顶点坐标分别是( )
| A. | 向下,(1,4) | B. | 向上,(1,4) | C. | 向下,(-1,-4) | D. | 向上,(-1,-4) |
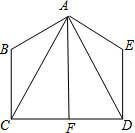 已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD.
已知,如图,AB=AE,∠B=∠E,BC=ED,∠CAF=∠DAF.求证:AF⊥CD.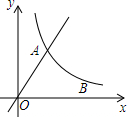 如图,直线y=$\frac{3}{4}$x与双曲线y=$\frac{k}{x}$(x>0)交于点A,将直线y=$\frac{3}{4}$x向右平移6个单位后,与双曲线y=$\frac{k}{x}$(x>0)交于点B,与x轴交于点C,若A点到x轴的距离是B点到x轴的距离的2倍,那么k的值为( )
如图,直线y=$\frac{3}{4}$x与双曲线y=$\frac{k}{x}$(x>0)交于点A,将直线y=$\frac{3}{4}$x向右平移6个单位后,与双曲线y=$\frac{k}{x}$(x>0)交于点B,与x轴交于点C,若A点到x轴的距离是B点到x轴的距离的2倍,那么k的值为( )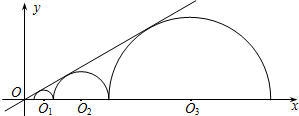 如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016=32015.
如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016=32015.