题目内容
8.若实数m、n满足4m2+12m+n2-2n+10=0,则函数y=x2m+4n+n+2是( )| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
分析 利用完全平方公式将所求的方程转化为a2+b2=0的形式,由非负数的性质求得m、n的值,然后代入求值即可.
解答 解:由4m2+12m+n2-2n+10=0,得
(2m+3)2+(n-1)2=0,
则2m+3=0,n-1=0,
解得 m=-$\frac{3}{2}$,n=1.
2m+4n=2×(-$\frac{3}{2}$)+4×1=1
所以 y=x2m+4n+n+2=y=x+3,即y=x+3,属于一次函数.
故选:B.
点评 本题考查了配方法的应用,非负数的性质和一次函数的定义.解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
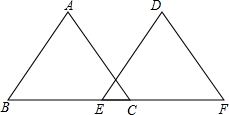 如图:B、E、C、F四点在同一直线上,且∠ACB=∠F,∠B=∠DEF,BE=CF,∠A=50°,求∠D的度数,并说明理由.
如图:B、E、C、F四点在同一直线上,且∠ACB=∠F,∠B=∠DEF,BE=CF,∠A=50°,求∠D的度数,并说明理由.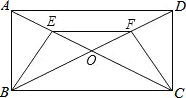 矩形ABCD的对角线AC、BD相交于点O,且AE=DF.
矩形ABCD的对角线AC、BD相交于点O,且AE=DF.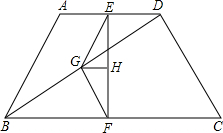 如图所示,已知:在四边形ABCD中,AB=CD,点E,F,G分别是AD,BC,BD的中点,GH平分∠EGF交EF于点H.
如图所示,已知:在四边形ABCD中,AB=CD,点E,F,G分别是AD,BC,BD的中点,GH平分∠EGF交EF于点H.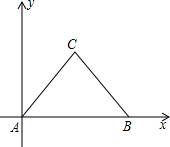 如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).
如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).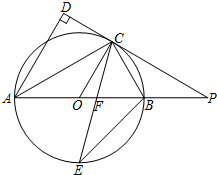 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.