题目内容
13.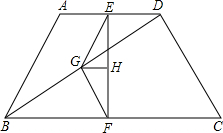 如图所示,已知:在四边形ABCD中,AB=CD,点E,F,G分别是AD,BC,BD的中点,GH平分∠EGF交EF于点H.
如图所示,已知:在四边形ABCD中,AB=CD,点E,F,G分别是AD,BC,BD的中点,GH平分∠EGF交EF于点H.(1)猜想:GH与EF之间的关系是GH⊥EF;
(2)证明你的猜想.
分析 可证明△GEF为等腰三角形,结合条件可证明GH⊥EF.
解答 (1)解:GH⊥EF;
(2)证明:∵G、E分别为BD、AD的中点,
∴GE是△ABD的中位线,
∴GE=$\frac{1}{2}$AB,
同理可得GF=$\frac{1}{2}$CD,
又AB=CD,
∴GE=GF,
又∵GH平分∠EGF交EF于点H,
∴GH⊥EF.
故答案是:GH⊥EF.
点评 本题主要考查三角形中位线定理和等腰三角形的性质,由中位线定理证得△GEF为等腰三角形是解题的关键.

练习册系列答案
相关题目
8.若实数m、n满足4m2+12m+n2-2n+10=0,则函数y=x2m+4n+n+2是( )
| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
5.如果(2x+y-2)2+|3x-2y-10|=0,那么x和y的值为( )
| A. | x=2,y=2 | B. | x=-2,y=2 | C. | x=-2,y=-2 | D. | x=2,y=-2 |
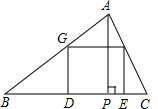 如图,△ABC是一块余料,BC=12cm,高AP=8cm.要把它加工成一块正方形材料,使正方形一边在BC上,其余两个顶点分别在AC、AB上.求这个正方形的边长是多少?
如图,△ABC是一块余料,BC=12cm,高AP=8cm.要把它加工成一块正方形材料,使正方形一边在BC上,其余两个顶点分别在AC、AB上.求这个正方形的边长是多少? 如图,等腰直角三角形ABC,∠A=90°,D是BC中点,E为AB上一点,且EA=CF,求证:DE=DF.
如图,等腰直角三角形ABC,∠A=90°,D是BC中点,E为AB上一点,且EA=CF,求证:DE=DF.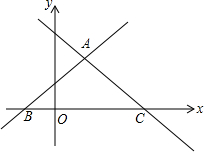 如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点.
如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点.