题目内容
20.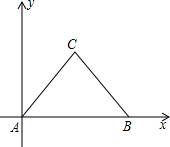 如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).
如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).
分析 根据题意画出图形,过点C作CD⊥x轴,先根据等边三角形的性质得出AC积AD的长,利用勾股定理即可得出结论.
解答 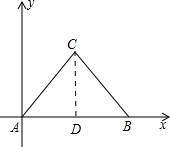 解:如图所示:过点C作CD⊥x轴,
解:如图所示:过点C作CD⊥x轴,
∵△ABC是等边三角形,B(6,0)
∴AC=6,AD=3,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴C(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).
故答案为:(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).
点评 本题考查的是等边三角形的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.求一个正数的算术平方根,有些数可以直接求得,如$\sqrt{4}$,有些数则不能直接求得,如$\sqrt{5}$,但可以通过计算器求.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:已知$\sqrt{2.06}$≈1.435,求下列各数的算术平方根:
①0.0206≈0.1435; ②20600≈143.5;
(3)根据上述探究过程类比研究一个数的立方根已知$\root{3}{2}$≈1.260,则$\root{3}{2000}$≈12.60.
| n | 16 | 0.16 | 0.0016 | 1600 | 16000 | … |
| $\sqrt{n}$ | 4 | 0.4 | 0.04 | 40 | 400 | … |
(2)运用你发现的规律,探究下列问题:已知$\sqrt{2.06}$≈1.435,求下列各数的算术平方根:
①0.0206≈0.1435; ②20600≈143.5;
(3)根据上述探究过程类比研究一个数的立方根已知$\root{3}{2}$≈1.260,则$\root{3}{2000}$≈12.60.
8.若实数m、n满足4m2+12m+n2-2n+10=0,则函数y=x2m+4n+n+2是( )
| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
5.如果(2x+y-2)2+|3x-2y-10|=0,那么x和y的值为( )
| A. | x=2,y=2 | B. | x=-2,y=2 | C. | x=-2,y=-2 | D. | x=2,y=-2 |
10.一个圆锥的底面半径为8cm,其侧面展开图的圆心角为240°,则此圆锥的侧面积为( )
| A. | 96πcm2 | B. | 48πcm2 | C. | 36πcm2 | D. | 24πcm2 |
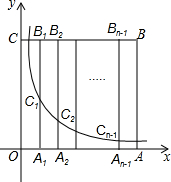 如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=$\frac{1}{x}$(x>0)于点C1,C2,…,Cn-1.BC与双曲线y=$\frac{1}{x}$交于点E,若$\frac{{B}_{n-1}E}{{B}_{n-1}{C}_{n-1}}$=$\frac{14}{15}$,则n的值为15.(n为正整数)
如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=$\frac{1}{x}$(x>0)于点C1,C2,…,Cn-1.BC与双曲线y=$\frac{1}{x}$交于点E,若$\frac{{B}_{n-1}E}{{B}_{n-1}{C}_{n-1}}$=$\frac{14}{15}$,则n的值为15.(n为正整数)