题目内容
19.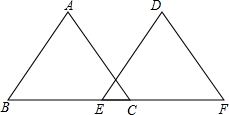 如图:B、E、C、F四点在同一直线上,且∠ACB=∠F,∠B=∠DEF,BE=CF,∠A=50°,求∠D的度数,并说明理由.
如图:B、E、C、F四点在同一直线上,且∠ACB=∠F,∠B=∠DEF,BE=CF,∠A=50°,求∠D的度数,并说明理由.
分析 已知△ABC与△DEF的两角相等,通过BE=CF可得BC=EF,即可判定△ABC≌△DEF(ASA),得到∠D=∠A=50°.
解答 证明:∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{∠ACB=∠F}\\{BC=EF}\\{∠B=∠DEF}\end{array}\right.$,
∴△ABC≌△DEF(ASA),
∴∠D=∠A=50°.
点评 本题主要考查三角形全等的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
10.求一个正数的算术平方根,有些数可以直接求得,如$\sqrt{4}$,有些数则不能直接求得,如$\sqrt{5}$,但可以通过计算器求.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:已知$\sqrt{2.06}$≈1.435,求下列各数的算术平方根:
①0.0206≈0.1435; ②20600≈143.5;
(3)根据上述探究过程类比研究一个数的立方根已知$\root{3}{2}$≈1.260,则$\root{3}{2000}$≈12.60.
| n | 16 | 0.16 | 0.0016 | 1600 | 16000 | … |
| $\sqrt{n}$ | 4 | 0.4 | 0.04 | 40 | 400 | … |
(2)运用你发现的规律,探究下列问题:已知$\sqrt{2.06}$≈1.435,求下列各数的算术平方根:
①0.0206≈0.1435; ②20600≈143.5;
(3)根据上述探究过程类比研究一个数的立方根已知$\root{3}{2}$≈1.260,则$\root{3}{2000}$≈12.60.
8.若实数m、n满足4m2+12m+n2-2n+10=0,则函数y=x2m+4n+n+2是( )
| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
 按下列语句画出图形
按下列语句画出图形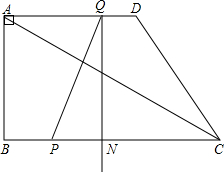 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=4,BC=7,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=4,BC=7,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒. 如图,等腰直角三角形ABC,∠A=90°,D是BC中点,E为AB上一点,且EA=CF,求证:DE=DF.
如图,等腰直角三角形ABC,∠A=90°,D是BC中点,E为AB上一点,且EA=CF,求证:DE=DF.
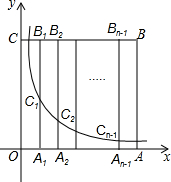 如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=$\frac{1}{x}$(x>0)于点C1,C2,…,Cn-1.BC与双曲线y=$\frac{1}{x}$交于点E,若$\frac{{B}_{n-1}E}{{B}_{n-1}{C}_{n-1}}$=$\frac{14}{15}$,则n的值为15.(n为正整数)
如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=$\frac{1}{x}$(x>0)于点C1,C2,…,Cn-1.BC与双曲线y=$\frac{1}{x}$交于点E,若$\frac{{B}_{n-1}E}{{B}_{n-1}{C}_{n-1}}$=$\frac{14}{15}$,则n的值为15.(n为正整数)