题目内容
17．解方程：$\frac{2-x}{x-3}$+2=$\frac{1}{x-3}$．分析 根据等式的性质，可得整式方程，根据解整式方程，可得方程的解．
解答 解：方程两边都乘以（x-3），得
2-x+2（x-3）=1．
解得x=5，
检验：把x=5代入（x-3）=2≠0，
故x=5是原方程的解．
点评 本题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解，注意解分式方程一定要验根．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
按下列语句画出图形
8．若实数m、n满足4m2+12m+n2-2n+10=0，则函数y=x2m+4n+n+2是（ ）
| A． | 正比例函数 | B． | 一次函数 | C． | 反比例函数 | D． | 二次函数 |
5．如果（2x+y-2）2+|3x-2y-10|=0，那么x和y的值为（ ）
| A． | x=2，y=2 | B． | x=-2，y=2 | C． | x=-2，y=-2 | D． | x=2，y=-2 |
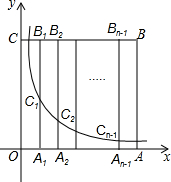如图，边长为n的正方形OABC的边OA，OC在坐标轴上，点A1，A2，…，An-1为OA的n等分点，点B1，B2，…，Bn-1为CB的n等分点，连结A1B1，A2B2，…，An-1Bn-1，分别交曲线y=$\frac{1}{x}$（x＞0）于点C1，C2，…，Cn-1．BC与双曲线y=$\frac{1}{x}$交于点E，若$\frac{{B}_{n-1}E}{{B}_{n-1}{C}_{n-1}}$=$\frac{14}{15}$，则n的值为15．（n为正整数）