Question

16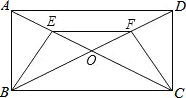．矩形ABCD的对角线AC、BD相交于点O，且AE=DF．
（1）求证：BE=CF；
（2）若E是AO的中点，AD=8cm，AB=4cm，求OF的长．

Answer 1

分析 （1）根据矩形对角线的性质，矩形对角线互相平分且相等，可知EO=FO，BO=CO，∠BOE=∠COF，可知△BOE≌△COF，即可得出BE=CF．
（2）由勾股定理求出BD=4$\sqrt{5}$cm，根据矩形的性质，即可解决问题．

解答 证明：（1）∵矩形ABCD的对角线为AC和BD，
∴AO=CO=BO=DO，
∵E、F分别是矩形ABCD的对角线AC和BD上的点，AE=DF，
∴EO=FO，
在△BOE和△COF中，
∵$\left\{\begin{array}{l}{EO=FO}\\{∠EOB=∠FOC}\\{BO=CO}\end{array}\right.$，
∴△BOE≌△COF（SAS），
∴BE=CF．

解：（2）由勾股定理得：BD²=AD²+AB²，
∵AD=4cm，AB=8cm，
∴BD=4$\sqrt{5}$（cm），
∵E是AO的中点，AE=DF，OA=OD，
∴点F是OD的中点，
∴OF=$\frac{1}{4}$×4$\sqrt{5}$=$\sqrt{5}$（cm）．

点评 该题主要考查了矩形的性质、全等三角形的判定及其性质、勾股定理等几何知识点的应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．