题目内容
6.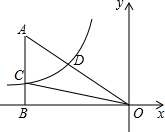 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )| A. | -4 | B. | -6 | C. | -9 | D. | -12 |
分析 设D(t,$\frac{k}{t}$),利用点D为OA的中点得到A(2t,$\frac{2k}{t}$),接着表示出C(2t,$\frac{k}{2t}$),然后根据三角形面积公式得到$\frac{1}{2}$•($\frac{2k}{t}$-$\frac{k}{2t}$)•(-2t)=9,再解关于k的方程即可.
解答 解:设D(t,$\frac{k}{t}$),
∵点D为OA的中点,
∴A(2t,$\frac{2k}{t}$),
∵AB⊥x,
∴C点的横坐标为2t,
∴C(2t,$\frac{k}{2t}$),
∴S△OAC=$\frac{1}{2}$•($\frac{2k}{t}$-$\frac{k}{2t}$)•(-2t)=9,
∴k=-6.
故选B.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
14.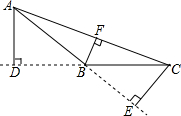 如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
 如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )| A. | $\frac{12}{5}$ | B. | 3 | C. | 4 | D. | 5 |
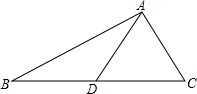 如图,AD是△ABC的中线.
如图,AD是△ABC的中线.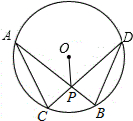 如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=50 度.
如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=50 度. 根据要求,用尺规作图:已知:∠AOB,点P在OA上,过点P作直线HD,使HD∥OB.(不写作法,保留作图痕迹)
根据要求,用尺规作图:已知:∠AOB,点P在OA上,过点P作直线HD,使HD∥OB.(不写作法,保留作图痕迹)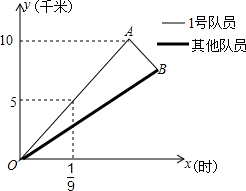 自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.
自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.