题目内容
3.在Rt△ABC中,∠B=90°,AB=1,BC=2,点E、F分别在边AB、AC上,连接EF,将△AEF沿EF翻折,使A落在BC上的D处,FD⊥BC,则ED=$\frac{5-\sqrt{5}}{4}$.分析 在Rt△ABC中,由勾股定理可知AC=$\sqrt{5}$,然后再证明AB∥FD,从而可知∠AEF=∠EFD,然后由折叠的性质可知:∠AEF=∠DEF,AE=DE,从而可证得AE=DF.
所以四边形AEDF为平行四边形,故此△BDE∽△BAC,由相似三角形的性质可知$\frac{BE}{AB}=\frac{ED}{AC}$,从而可求得DE=$\frac{5-\sqrt{5}}{4}$.
解答 解:如图所示: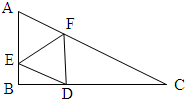
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵FD⊥BC,
∴∠FDC=90°.
∴∠FDC=∠B.
∴AB∥FD.
∴∠AEF=∠EFD.
由折叠的性质可知:∠AEF=∠DEF,AE=DE.
∴∠EFD=∠DEF.
∴ED=DF.
∴AE=DF.
∴四边形AEDF为平行四边形.
∴AF∥ED.
∴△BDE∽△BAC.
∴$\frac{BE}{AB}=\frac{ED}{AC}$,即$\frac{1-x}{1}=\frac{x}{\sqrt{5}}$.
解得:x=$\frac{5-\sqrt{5}}{4}$.
∴DE=$\frac{5-\sqrt{5}}{4}$.
故答案为:$\frac{5-\sqrt{5}}{4}$.
点评 本题主要考查的是折叠的性质、勾股定理、相似三角形、平行四边形的性质和判定的综合应用,证得四边形AEDF为平行四边形,从而得到△BDE∽△BAC是解题的关键..

练习册系列答案
相关题目
14.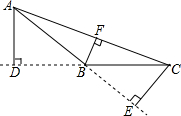 如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
 如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )| A. | $\frac{12}{5}$ | B. | 3 | C. | 4 | D. | 5 |
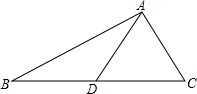 如图,AD是△ABC的中线.
如图,AD是△ABC的中线.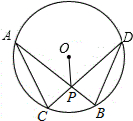 如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=50 度.
如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=50 度. 根据要求,用尺规作图:已知:∠AOB,点P在OA上,过点P作直线HD,使HD∥OB.(不写作法,保留作图痕迹)
根据要求,用尺规作图:已知:∠AOB,点P在OA上,过点P作直线HD,使HD∥OB.(不写作法,保留作图痕迹)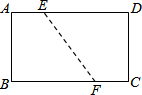 如图,在矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,则折痕EF的长为7.5.
如图,在矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,则折痕EF的长为7.5.