题目内容
某书店以每本20元的价格购进一批畅销书《莫言精品集》.销售过程中发现,每月销售量y(本)与销售单价x(元)之间的关系如下表所示,按照表中y与x的关系规律,解决下面的问题
(1)每月销售量y与销售单价x满足我们学习过的三种函数(即一次函数、反比例函数和二次函数)关系中的一种.试求出y与x之间的函数关系式,不要求写出自变量x的取值范围.
(2)销售单价在什么范围时,书店不亏损?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
| x | 25 | 28 | 30 | 32 | 35 |
| y | 250 | 220 | 200 | 180 | 150 |
(2)销售单价在什么范围时,书店不亏损?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)
考点:一次函数的应用
专题:
分析:(1)设每月销售量y与销售单价x之间的函数关系式为y=kx+b,由待定系数法求出其解即可;
(2)设书店的利润为w,由利润=每本书的利润×数量就可以得出解析式,再由解析式建立不等式求出其解即可;
(3)由(2)的解析式建立不等式,求出其解即可.
(2)设书店的利润为w,由利润=每本书的利润×数量就可以得出解析式,再由解析式建立不等式求出其解即可;
(3)由(2)的解析式建立不等式,求出其解即可.
解答:解:(1)设每月销售量y与销售单价x之间的函数关系式为y=kx+b,由题意,得
,
解得:
,
∴y与x之间的函数关系式为y=-10x+500;
(2)设书店的利润为w,由题意,得
w=(-10x+500)(x-20),
w=-10x2+700x-10000,
当w≥0时,
-10x2+700x-10000≥0,
(x-20)(x-50)≤0
解得:20≤x≤50.
答:销售单价在20≤x≤50范围时,书店不亏损;
(3)由题意,得
-10x2+700x-10000≥2000,
解得:30≤x≤40
当x=30时,y=200,
∴成本为:200×20=4000,
当x=40时,y=100,
∴成本为:20×100=2000.
∵2000<4000,
∴该书店每月的成本最少需要2000元.
|
解得:
|
∴y与x之间的函数关系式为y=-10x+500;
(2)设书店的利润为w,由题意,得
w=(-10x+500)(x-20),
w=-10x2+700x-10000,
当w≥0时,
-10x2+700x-10000≥0,
(x-20)(x-50)≤0
解得:20≤x≤50.
答:销售单价在20≤x≤50范围时,书店不亏损;
(3)由题意,得
-10x2+700x-10000≥2000,
解得:30≤x≤40
当x=30时,y=200,
∴成本为:200×20=4000,
当x=40时,y=100,
∴成本为:20×100=2000.
∵2000<4000,
∴该书店每月的成本最少需要2000元.
点评:本题考查了运用待定系数法求函数的解析式的运用,销售问题的数量关系的运用,一元二次不等式的运用,解答时求出函数的解析式是关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
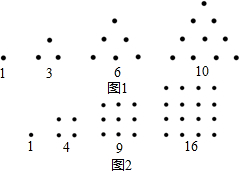 希腊人常用小石子在沙滩上摆成各种性状来研究数,
希腊人常用小石子在沙滩上摆成各种性状来研究数,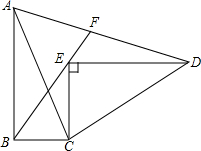 Rt△ABC≌Rt△DEC,∠ABC=∠DEC=90°,BE的延长线交AD于点F,求证:AF=DF.
Rt△ABC≌Rt△DEC,∠ABC=∠DEC=90°,BE的延长线交AD于点F,求证:AF=DF.