题目内容
今年我市的蔬菜市场从5月份开始,由于本地蔬菜的上市,某种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数:y=-
x2+bx+c.
(1)求出5月份y与x所满足的二次函数关系式;
(2)若5月份的进价m(元/千克)与周数x所满足的函数关系为m=-0.2x+2.求出5月份销售此种蔬菜一千克的利润W(元)与周数x的函数关系式,并求出在哪一周销售此种蔬菜一千克的利润最大?且最大利润是多少?
| 1 |
| 20 |
(1)求出5月份y与x所满足的二次函数关系式;
(2)若5月份的进价m(元/千克)与周数x所满足的函数关系为m=-0.2x+2.求出5月份销售此种蔬菜一千克的利润W(元)与周数x的函数关系式,并求出在哪一周销售此种蔬菜一千克的利润最大?且最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)把x=1,y=2.8和x=2,y=2.4,分别代入y=-
x2+bx+c可求b、c的值,确定二次函数解析式;
(2)根据一次函数,二次函数的性质及自变量的取值范围,求最大利润.
| 1 |
| 20 |
(2)根据一次函数,二次函数的性质及自变量的取值范围,求最大利润.
解答:解:(1)将(1,2.8)(2,2.4)代入y=-
x2+bx+c.
可得:
,
解得:
,
即y=-
x2-
x+3.1.
(2)5月份此种蔬菜利润可表示为:W=y-m=(-0.05x2-0.25x+3.1)-(-0.2x+2),
即:W=-0.05x2-0.05x+1.1
由函数解析式可知,五月份的利润随周数变化符合二次函数且对称轴为:x=-
=-
,
即在第1至4周的利润随周数的增大而减小,所以应在第一周的利润最大,最大为:W=-0.05-0.05+1.1=1(元/千克).
| 1 |
| 20 |
可得:
|
解得:
|
即y=-
| 1 |
| 20 |
| 1 |
| 4 |
(2)5月份此种蔬菜利润可表示为:W=y-m=(-0.05x2-0.25x+3.1)-(-0.2x+2),
即:W=-0.05x2-0.05x+1.1
由函数解析式可知,五月份的利润随周数变化符合二次函数且对称轴为:x=-
| b |
| 2a |
| 1 |
| 2 |
即在第1至4周的利润随周数的增大而减小,所以应在第一周的利润最大,最大为:W=-0.05-0.05+1.1=1(元/千克).
点评:本题考查了二次函数解析式求法及二次函数的实际应用,解答本题的关键是求出两函数关系式,将实际问题转化为数学计算,有一定难度.

练习册系列答案
相关题目
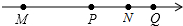 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )| A、点M | B、点N | C、点P | D、点Q |
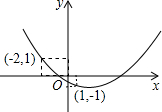 如图,二次函数y=ax2+bx+c的图象经过点(1,-1)和(-2,1),下列关于此二次函数的叙述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,-1)和(-2,1),下列关于此二次函数的叙述,正确的是( )| A、当x=0时,y的值小于-1 |
| B、当x=-3时,y的值大于1 |
| C、当x=5时,y的值等于0 |
| D、当x=1时,y的值大于1 |
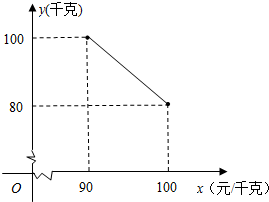 某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律. 在直角坐标系中,等边三角形AOB的位置如图所示,等边三角形的边长为2,求△AOB各顶点的坐标.
在直角坐标系中,等边三角形AOB的位置如图所示,等边三角形的边长为2,求△AOB各顶点的坐标.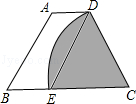 如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )
如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )
 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4