题目内容
 希腊人常用小石子在沙滩上摆成各种性状来研究数,
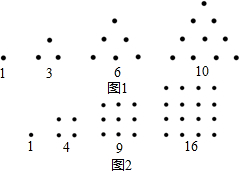
希腊人常用小石子在沙滩上摆成各种性状来研究数,例如:
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中既是三角形数又是正方形数的是( )
| A、289 | B、1024 |
| C、1225 | D、1378 |
考点:规律型:图形的变化类,规律型:数字的变化类
专题:
分析:由题意可知:三角形数的第n个为1+2+3+4+…+n=
n(n+1),正方形数的第n个为n2,由此逐一验证得出答案即可.
| 1 |
| 2 |
解答:解:由于三角形数的第n个为1+2+3+4+…+n=
n(n+1),正方形数的第n个为n2,
A、
n(n+1)=289无整数解,不合题意;
B、
n(n+1)=1024,不合题意;
C、
n(n+1)=1225,解得n=49,符合题意;
D、
n(n+1)=1378,无整数解,不合题意.
故选:C.
| 1 |
| 2 |
A、
| 1 |
| 2 |
B、
| 1 |
| 2 |
C、
| 1 |
| 2 |
D、
| 1 |
| 2 |
故选:C.
点评:此题考查图形的变化规律,找出图形之间的联系,利用数字之间的运算规律,解决问题.

练习册系列答案
相关题目
 如图,⊙A,⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )
如图,⊙A,⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )A、
| ||
B、
| ||
| C、π | ||
| D、π |
某种商品的进价为每件180元,现按标价的九折销售时,利润率为15.2%,就这种商品的标价为每件x元,依题意列方程正确的是( )
| A、180-0.9x=180×15.2% |
| B、0.9x=180×15.2% |
| C、0.9x-180=180×15.2% |
| D、15.2%x=180×0.9 |
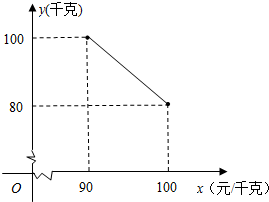 某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.