题目内容
6.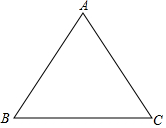 如图,等边△ABC的边长为6,
如图,等边△ABC的边长为6,(1)求作它的内切圆⊙O;
(2)求⊙O的半径.
分析 (1)分别作BC和AC的垂直平分线,它们相交于点O,利用△ABC为等边三角形可得到点O为△ABC的内心;
(2)利用作法得BH=CH=3,在利用△ABC为等边三角形得到∠OBH=30°,然后根据直角三角形三边的关系计算出OH即可.
解答 解:(1)如图,点O为所作;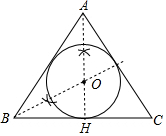
(2)∵点O为BC和AC的垂直平分线的交点,
∴BH=CH=3,
∵△ABC为等边三角形,
∴OB平分∠ABC,
∴∠OBH=30°,
在Rt△OBH中,OH=$\frac{\sqrt{3}}{3}$BH=$\sqrt{3}$.
∴⊙O的半径为$\sqrt{3}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等边三角形的性质和三角形的内心.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.已知A、B在数轴上分别表示a、b.
(1)对照数轴填写表格:
(2)若A、B两点间的距离记为d,试问d和a、b(a<b)有何数量关系;
(3)求出数轴上到7和-7的距离之和为14的所有整数的和;
(4)若点C表示的数为x,当点C在什么位置时,|x+1|+|x-2|取得的值最小.
(5)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).求两个动点运动的速度.
(1)对照数轴填写表格:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)求出数轴上到7和-7的距离之和为14的所有整数的和;
(4)若点C表示的数为x,当点C在什么位置时,|x+1|+|x-2|取得的值最小.
(5)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).求两个动点运动的速度.
 通州广场上有一旗杆,你能用一些简易的工具,根据全等三角形的有关知识,测出旗杆的高吗?画出示意图,并作说明.
通州广场上有一旗杆,你能用一些简易的工具,根据全等三角形的有关知识,测出旗杆的高吗?画出示意图,并作说明.
 已知:一次函数y=-x+8与两坐标轴分别交于A、B点,P为线段AB上的任意一点,过P点作PE⊥OA于点E,作PF⊥OB于F点,当长方形PEOF的面积最大时,P点坐标为(4,4).
已知:一次函数y=-x+8与两坐标轴分别交于A、B点,P为线段AB上的任意一点,过P点作PE⊥OA于点E,作PF⊥OB于F点,当长方形PEOF的面积最大时,P点坐标为(4,4).