题目内容
11．
已知：一次函数y=-x+8与两坐标轴分别交于A、B点，P为线段AB上的任意一点，过P点作PE⊥OA于点E，作PF⊥OB于F点，当长方形PEOF的面积最大时，P点坐标为（4，4）．
分析 设点P的坐标为（x，-x+8），继而根据矩形的面积公式可用含x的代数式表示长方形PEOF的面积，再利用配方法确定最值即可．
解答 解：设点P的坐标为（x，-x+8），
长方形PEOF的面积为x（-x+8）=-x2+8x=-（x-4）2+16，
∵0＜x＜8，
∴当x=4时，长方形PEOF的面积取得最大值，点P坐标为（4，4）．
故答案为：（4，4）．
点评 本题考查了一次函数图象上点的坐标特征，解答本题的关键是熟练点的坐标与线段长度之间的转化，掌握矩形的面积计算公式，总体来说本题难度不大．
练习册系列答案
字词句段篇系列答案
相关题目
19．
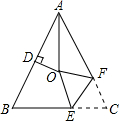如图，△ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数是（ ）
如图，△ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数是（ ）| A． | 100° | B． | 108° | C． | 120° | D． | 126° |
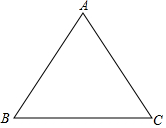如图，等边△ABC的边长为6，
如图所示，A、B两点的坐标分别是A（1，$\sqrt{2}$），B（$\sqrt{5}$，0），如果把A、B两点的纵、横坐标都同时扩大2倍．
抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点是点A（3，0），其部分图象如图，则下列结论：