题目内容

14．已知二次函数y=x2-6x+8．
（1）将解析式化成顶点式；
（2）写出它的开口方向、对称轴和顶点坐标；
（3）x取什么值时，y随x的增大而增大；x取什么值时，y随x增大而减小．

分析 （1）利用配方法将解析式化成顶点式；
（2）根据二次函数的性质解答；
（3）根据抛物线的开口方向、对称轴以及二次函数的性质解答．

解答 解：（1）y=x2-6x+8=x2-6x+9-1=（x-3）2-1；
（2）开口向上，对称轴是x=3，顶点坐标是（3，-1）；
（3）x＞3时，y随x的增大而增大；x＜3时，y随x增大而减小．

点评 本题考查的是二次函数的三种形式、配方法的应用以及二次函数的性质，灵活运用配方法把一般式化为顶点式是解题的关键．

练习册系列答案
相关题目
4．如图，已知OP平分∠AOB，用直尺和圆规作图
（1）作PD⊥OB，垂足为D；
（2）作PC⊥OP交OA于点C．
5．若a，b，c是△ABC的三边长，且a，b，c满足（a-5）2+（b-12）2+|c-13|=0．
（1）求a，b，c的值；
（2）△ABC是直角三角形吗？请说明理由．
2．把下列各数填在相应的表示集合的大括号内
-2，-$\frac{1}{3}$，-|-3|，$\frac{22}{7}$，-0.3，1.7，0，-（-5），8
分数{-$\frac{1}{3}$，$\frac{22}{7}$，-0.3，1.7 …}
负分数{-$\frac{1}{3}$，-0.3…}
整数{-2，-|-3|0，-（-5）8 …}
自然数{0，-（-5），8 …}．
9．计算：
（1）（$\sqrt{5}$+1）（$\sqrt{5}$-1）+（-2）0-$\root{3}{27}$；
（2）|-$\sqrt{2}$|+$\sqrt{9}$×（$\frac{1}{2}$）-1-$\sqrt{4}$×$\sqrt{\frac{1}{2}}$-（π-1）0．
19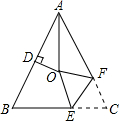．如图，△ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数是（　　）
A．100°B．108°C．120°D．126°
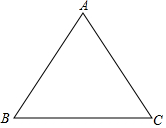6．如图，等边△ABC的边长为6，
（1）求作它的内切圆⊙O；
（2）求⊙O的半径．
3．把下列各数填入它所在的数集内：-$\frac{22}{7}$，-$\frac{π}{2}$，-0.1010010001…，0，-（-2.28），-|-4|，-32
正数集合：{-（-2.28）…} 
负分数集合：{-$\frac{22}{7}$…}
非正整数集合：{0，-|-4|，-32…}
无理数集合：{-$\frac{π}{2}$，-0.1010010001……}．
4．如果向东走2km记作+2km，那么-5km表示向西走5km．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网