题目内容
如果b-a=2,c-d=3,求a2-ab+b2-bc+c2-ca的值.
考点:因式分解的应用
专题:计算题
分析:原式利用完全平方公式变形,把各自的值代入计算即可求出值.
解答:解:∵b-a=2,c-b=3,
∴b-a+c-b=c-a=5,
则a2-ab+b2-bc+c2-ca=2(a2-ab+b2-bc+c2-ca)
=
(a2+b2-2ab+b2+c2-2bc+a2+c2-2ac)
=
[(a-b)2+(b-c)2+(a-c)2]
=
×(4+9+25)
=19.
∴b-a+c-b=c-a=5,
则a2-ab+b2-bc+c2-ca=2(a2-ab+b2-bc+c2-ca)
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=19.
点评:此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 农村长搭建横截面为半圆的全封闭塑料薄膜蔬菜大棚,如图所示,如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是( )m2.
农村长搭建横截面为半圆的全封闭塑料薄膜蔬菜大棚,如图所示,如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是( )m2.| A、60π | B、78π |
| C、64π | D、120π |
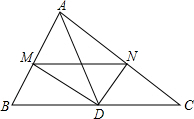 在△ABC中,AD是中线,DM是∠ADB的平分线,交AB于M,DN是∠ADC的平分线交AC于N点.求证:BM+CN>MN.
在△ABC中,AD是中线,DM是∠ADB的平分线,交AB于M,DN是∠ADC的平分线交AC于N点.求证:BM+CN>MN. 如图,AB为圆O的直径,C为圆O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E,CF⊥AB于点F.
如图,AB为圆O的直径,C为圆O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E,CF⊥AB于点F.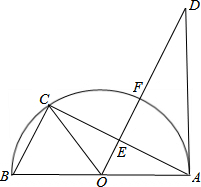 如图,AB是半圆O的直径,点C在半圆O上,过点O作OD∥BC交圆的切线AD于点D,交弦AC于E,交半圆于点F.
如图,AB是半圆O的直径,点C在半圆O上,过点O作OD∥BC交圆的切线AD于点D,交弦AC于E,交半圆于点F.