题目内容
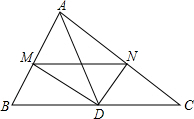 在△ABC中,AD是中线,DM是∠ADB的平分线,交AB于M,DN是∠ADC的平分线交AC于N点.求证:BM+CN>MN.
在△ABC中,AD是中线,DM是∠ADB的平分线,交AB于M,DN是∠ADC的平分线交AC于N点.求证:BM+CN>MN.考点:全等三角形的判定与性质,三角形三边关系
专题:证明题
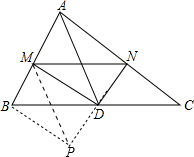
分析:延长ND至P,使DP=ND,连结MP、BP,易证△BDP≌△CDN,根据全等三角形对应边相等的性质,线段中垂线定理可得MN=MP,再根据三角形三边关系即可求解.
解答:证明:延长ND至P,使DP=ND,连结MP、BP,
∵点D为BC的中点,
∴BD=CD,
在△BDP与△CDN中,
,
∴△BDP≌△CDN(SAS),
∴PB=CN,
∵MD⊥PN,DP=DN,
∴MN=MP(线段中垂线定理),
∵BM+BP>MP,
∴BM+CN>MN.

∵点D为BC的中点,
∴BD=CD,
在△BDP与△CDN中,
|
∴△BDP≌△CDN(SAS),
∴PB=CN,
∵MD⊥PN,DP=DN,
∴MN=MP(线段中垂线定理),
∵BM+BP>MP,
∴BM+CN>MN.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BDP≌△CDN是解题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
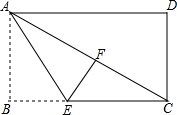 如图,在长方形ABCD中,AB=6,BC=8,先将矩形沿对角线折叠,再将矩形沿AE对折,使点B落在AC边的点F处,求折痕AE的长.
如图,在长方形ABCD中,AB=6,BC=8,先将矩形沿对角线折叠,再将矩形沿AE对折,使点B落在AC边的点F处,求折痕AE的长.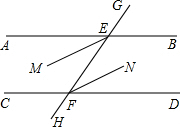 如图,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD.
如图,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD.